AtCoder にぼしの解いた問題たち(随時更新)
AtCoder 解いた問題一覧
他記事へのリンク
更新情報
2021/08/08
前書き
AtCoderで解いていった問題の解き方（簡易版）をまとめていく この問題、あの問題みたいにやれば解けそう！！って時にココ見れば分かる。って感じにしたい。
あくまで自分用ですが、アドバイス等は遠慮なくもらえると嬉しいです。
リンク切れ等ございましたらご報告ください！！！ コードは特に記述のない限りc++14(GCC5.4.1)です
使い方
"Ctrl + f" で検索窓を開いて、「DP」みたいな感じで検索してね。
問題名で検索することも可能です。
構成
- 解いた問題のタイトル
- 一言コメント
ABC
ABCのB問題のいくつかを埋めたときの記録 ここには, ABC001 / ABC003 / ABC006 / ABC009 / ABC010 / ABC011 / ABC012 / ABC013 / ABC014 / ABC018 / ABC020 / ABC021 / ABC022 / ABC024 / ABC025 / ABC027 / ABC028 / ABC033 / ABC035 / ABC036 / ABC037 / ABC038 / ABC040 / が入っています。
abc042B - 文字列大好きいろはちゃんイージー / Iroha Loves Strings (ABC Edition)
vectorに入れてソートする問題
abc043B バイナリハックイージー / Unhappy Hacking (ABC Edit)
string 文字列に対しても、pop_back()という関数を用いることが出来る ちなみにこれ、空の文字列に対して行ったらどうなるんだろうね！！（気になる）
abc047 一次元リバーシ / 1D Reversi
同じ文字のまとまりを1つの区画として、何区画あるか数え上げる 特別なことはしていない
abc51c Back and forth**
abc056 Go Home
ちょっとずつ動ける範囲が広くなる 負の方向に跳ねるのは無駄だ
abc058 Dubious Document / 怪文書
その文字が何回出てきたかを数える 英小文字と数字を対応させる。 mapでも解けそう
abc061C Big Array
制約が緩いので配列サイズNで、配列の要素番号と値を対応させて間に合う問題。
abc067 Splitting Pile
整数列が与えられて、前から値を足していったとき、その整数列の総和の半分に値を近づける。
abc073C Write and Erase
出てくる回数が奇数か偶数かを見るだけ mapを使った
abc088C Takahashi`s Information
数学チックな問題 連立方程式を使うのかな
abc110C String Transformation (niboshi time 35m)
難しかった。 サンプルを見て頭を回せ。 全ての出現する文字に対して、対応するものは1個だけじゃないといけない 解説動画で感動するが、これは悩んだものに与えられる特権
abc094D Binomial Coefficients
直感的にやったらＡＣしてしまった問題。 二項係数に関する問題、証明がなかなか面白い（？）ので公式解説を見るのをお勧めする。
abc110D Factorization
解けてうれしくなれた。 良い記事を書いたよ。 数え上げの問題。逆元も使う。（逆元の解説はない）
abc116 Grand Garden
操作をする系問題（おおざっぱかよ） 左からどんどん花を完成させていくっていう方針で大体いいと思う。
abc128c Switches
bit全探索 bit全探索の初級と言われればそうかもしれないが、bit全探索初心者にとっては結構難しい 僕にとっても難しい。
abc131 Megalomania
Yes,No問題、締め切りが近い順にやっていけばいい 証明は分からないけど直感がそう言ってる とか言って証明はURL飛べばある（あるよ）
abc146
記事 (記事はD問題まで書きました) 二冠 二分探索何もわかってなかった。 ABC回の参加の方針が少し経った気がする
ARC
arc059 いっしょ / Be Together (メンヘラ）
記事 全探索（簡単）
ARC068C - X: Yet Another Die Game
記事 計算量1の問題 記念すべき400AC目 最適な操作方法に気付けるか
arc069 Scc Puzzle
ARC073c Sento
記事 押すとT秒水が流れるボタンをたくさんの人が止まってからや止まる前に押したとき、合計で何秒流れるかの問題 ・水が流れ始めてから次に押す人が何秒後に押すかに着目 難しい文法はない
arc091c Flip,Flip,and Flip
計算量が1の問題 表になるものを数える もしくは裏になるものを数える 自身を含めて周りにマスが偶数個あれば操作が偶数回で表 奇数個なら裏。
AGC
agc002 Box and Boal
割と面白い問題、AGCだけど古い問題なのでdifficultyほどの難しさはない印象。 実装系だと思う 入力で与えられる添え字-1 が配列で見たいところっていうのに気づかずちょっと手間がかかった。
agc006 Prefix and Suffix
substrを使うと綺麗かな 二つの文字列 S , Tに対して Sの後ろ側と Tの前側で一致する文字列の長さの最大値が答えに関連する
agc011 Airport Bus
sortして、到着するのが早い人からどんどん処理をしていく。 難しい構文は使っていない。
agc013 Sorted Arrays
実装が難しい問題（？） 数列が与えられて、期待する数列に分けるにはどうしたらいいか？みたいな
agc015A A+...+B Problem
考察の問題 計算量1の問題 和を最大値と最小値まで、任意の値にすることが出来る（できるので）
agc015B Evilator
記事 難しいことはしていない どの階にも1回か2回押せばいける。
agc022 Diverse Word
記事 解説通りには解けていないが嘘解法ではないはず。 辞書順なのでnextpermutationを使った 文字列の長さがアルファベットの数と同じ26であるときの考えが難しい next_permutationは自分で実装すると案外難しいのでやってみると面白い（らしい）いつかやってみよう
agc031A
記事 難しい文法は使ってないけど難しい問題 文字列が与えられて考えられる文字列？が何通りあるか数える abcd ⇒ a , b , c, d, ab, ac, ad , bc,bd,cdk, abc, abd ,acd, bcd , abcd で15通り みたいなやつ
agc032A Limited Insertion
記事 vectorの要素の削除を初めて使った。 くそ難しい問題なので、何か新しく理解出来たら追加で何かをかきたい
日ごとのまとめ
12月4日
ABC028c - 数を三つ選ぶマン
ABC136d - Gathering Children
これらは article,12月4日 の中にまとめてぶち込んでます
12月5日
技術室億プログラミングコンテスト#4 Day1 a- ヘビがヘビー
技術室億プログラミングコンテスト#4 Day1 B- Long Long Ago
ABC142 E-Get Everything
三つの記事について書いたの記事はこちら～にぼしの記事
Get Everything は写経AC。集合を二進数で扱うbitDP、配るDP。どの鍵を使うかで全探索はできないが、 箱が開いているか開いてないかの状況で全探索はできる。 一つ前の状況から、カギを使うことであらわされる二進数表記の状態を考える
面白い問題！！（写経ACだけど）
abc064 D - Insertion 難しい
文字列操作系の問題（苦手）
どこに挿入するかがポイント？
12月6日
diverta 2019 Programming Contest C- AB substrings
diverta C-AB substrings 悪くない問題
文字列操作系の問題 簡単か難しいって言われたよくわからないけど 慣れてはや解き出来るようになろうねって感じ
12月8日
- 解いた問題 ABC010C-浮気調査
ARC029 A-高橋くんとお肉
C - Digits in Multiplication
浮気と調査
距離を求めるときは doubleを使おうね
高橋くんとお肉 bit 全探索
最近はbit全探索の問題をよく見かけるようになってきた。 やはり同じぐらのでぃフィカルティには同じ位の難易度の問題が集まるのだろうか？
12月9日
- 解いた問題 C - Dubious Document 2
ABC076C - Dubious Document 2 [substr,部分文字列、貪欲、辞書順最小] '?'は'a'にしたほうが辞書順最小になる 最低でもtを一つ部分文字列に含んでいればいいので,tとして考えられる場所が複数ある場合は、 できるだけ後ろのほうが良い。 (前が'a'になっていた方が辞書順で早いので
ABC041C - 背の順
ABC029 C- Brute-force Attack [next_permutation] next_permutationの手動実装みたいなノリ
ARC016 B- 音楽ゲーム
AGC005 A- STring 難しめ
ABC147 C -HonestOrUnkind2 ビット全探索！！
ABC108 C- Trianglular Relationship 写経AC
ABC033 C- 数式の書き換え
CODE FESTIVAL 2016 qual C B-K Cakes ちょっとだけ頭を使う
AGC011 B - Colorful Creatures 楽しい
Dubious Document、 substrを使う問題
substrが使えそうって思ったとき、使い慣れてないせいで別解法に逃げがち（WA出した） おとなしくsubstr使えるようになろうね
12月10日
- 解いた問題一覧 ABC127 D- Integer Cards
ABC085 D- Katana Thrower 上二問は似ているぞ。
Tenka1 Programmer Beginner Contest 2019
D - Rain Flows into Dams
ABC114 C-755 写経AC
12月11日
- 解いた問題
- ABC069 C- 4- adjacent
- ARC003 B-さかさま辞書
- ABC134 D- Preparing Boxes 多分これが一番おもしろかった 後ろから球を入れてくのがいい 12月11日の記事はこちら
12月12日
- 解いた問題
- ABC112 D-Partition [最大公約数,天才考察,]
12月12日の記事 全然やってない；；
12月14日
- 解いた問題
- ARC054 A- 動く歩道 次の問題に比べればかんたんな条件分岐
- ARC051 A- 塗り絵 勘弁してくれ。図形の問題。直線と円 なんかかっこいい解き方あるのかね
12月15日
- 解いた問題
- diverta 2019 Programming Contest 2 B-Picking Up マップのキーはペアでもいいよって言う
12月16日
- 解いた問題
- ARC043 A-点数変換
REが出ないせいでやられた。少数嫌い 12月16日の記事
いつ解いたか分からないやつ
ARC007迷子のCDケース
[MAP] なんかうまく行かない。 n個のCDに対して n-1個のCDケースと1個のカセット。 CDケースの番号とCDの番号を対応付けて、カセットをCDケース0。 disk0 ~ disk m-1 に対して、以下のような操作を行う
disk[i] = k ,現在流れている曲を p とすると kが入っているケースにpを入れ,pが入っているケース（つまりカセット）にkを入れる
ポイントは,kが入っているケースを見つけるために線形探索を行わなければいけないってこと cd[i] にはi番目のケースに入っているCDの番号を入れる。(0 <= i <= n)
ABC079 D-Wall
[ワーシャルフロイド法] https://atcoder.jp/contests/abc079/tasks/abc079_d 頂点間を結ぶ最短距離（経路を求める） 書き方は考えるのちょっときついから覚えちゃったほうが良いらしい. 計算量は頂点の数の3乗 rep(k,v){ rep(i,v){ rep(j,v){ dist[i][j] = min(dist[i][j] , dist[i][k] + dist[k][j]); } } }
Caddi2018 D- Harlequin
ゲームの必勝法。なるほど面白い。 全部偶数で自分の手番が始まりさえすれば、相手の動きを真似することで、コマが全部なくなるのは自分のターンにできる。 なるほどな
2020/01/27
1月入ってからずっと書くのサボってました ぼちぼちやろうね。
ABC153 E-Crested Ibis VS Monster
[DP Dynamic Proggramming, 動的計画法] DPっぽいよなあ。って問題。 解説動画によると、二次元DPでも一次元DPでも行けるとのこと。 とりあえず頑張って二次元で書けと言われたので書いた。 提出コード こーどの コレがないと 死ぬ ってやつを忘れるとWAです。 dp[i][j] := i番目までの魔法でjのダメージ（以上）を与えるときの最小のMP消費量。なので if (j == 0 ) では、0ダメージ以上なので魔法を使わなくて良いんだよ。
動的計画法,dpはdp[i][j] := hoge って定義考えるとちょっと見通しが良くなる気がする。 あと、これのコードの記事も書きました
ABC152 D - Handstand 2
[数え上げ, MAP,回文] 数字の上位と下位の数字（100433543 なら上位は１ 下位は３）を見て、与えられた範囲内で下位で始まり上位で始まるものが何個あるかを数える問題 (カッコ内の例の場合は 31 ,331, 311…みたいなものの数を数える） 雑に言うと、１回目のループで1からnまでの数字について、それぞれが何で始まり(上位がなにで）何で終わるか(下位が何か）を全部作っていく。 そして、２回目のループで、1からnまでの数字について,aで始まりｂで終わるなら、ｂで始まりaで終わるものの数を数えていく。
2月１日 貪欲消化回〜〜〜
[貪欲,greedy] にぼしくん,蟻本をやろうということで、某ちょんさんが蟻本の問題をAtCoderの問題に対応付けてくれているので、それを消化していきます！！ ところで貪欲法って使えることの証明が大事だと思うんですよね。分かる？人間の諸君
ABC083 C-Multiple Gift
[貪欲] Xから２倍、その値を２倍ってやっていくのが最適な貪欲ですよね〜〜（証明貪欲)
証明しないとまずいな、ってことで、公式の解説に証明載っていたので写経しました。 画像を直接貼るのめんどくさいのでTwitterのリンクにします C-Multiple Gift 証明
ARC006 C-積み重ね
[貪欲] 最初これ、入力与えられてきている順番にダンボールを積まないといけないっていうところに気が付きませんでした。
普通に思い順に１山にしたらよくない？って思ってしまいましたね。 これまた証明が思い浮かばない… そしてまた、感覚でも納得できないですね。
っていうことで解説読んで証明を理解してきましょう。
まあ、偉そうに写経なんて載せてますけど公式の解説写経です。これが一番しっくり北
ABC005 C- おいしいたこ焼きの売り方
[貪欲,二部グラフの最大マッチング] (↑ タグはつけてますけど、貪欲以外では解いていないです。） なんとなく、証明以外の部分はちゃんとルールを決めて解こうと考察できたと思う 考察用紙貼っておきます。
どんな貪欲か,以下のルールでタコ焼きを売り続けます
- B[0]から、B[m-1]（m人の客）について、売れるたこ焼きがある時は、可能な限り古いたこ焼きを提供する。
あいも変わらず、証明はできないので、公式の解説を写経してみる。 写経してみた
2020/02/02
ABC103 D-Islands War [区間スケジューリング,貪欲,greedy,] 難しいですね。 お得に橋を切ることを考えているのですが、言語化ができなくて苦労している問題。 自力で解けたんだけど、なんか上手い解説は浮かばない。 公式の解説を見ようね
2020/02/03
ABC132 D- Blue and Red Balls
[コンビネーション、組み合わせ数え上げ、mod、nCm,DP,動的計画法、パスカルの三角形] nCmは普段良くわからない方法で求めてるけど、解説どおりパスカルの三角形で実装してみた。 多分これあらがありまくる。 あらがありすぎて新垣ゆいになりそうなレベル。
2020/02/19
ABC126 D-Even Relation
[グラフ、二部グラフ、DFS]
隣の頂点との距離が偶数か奇数か グラフの問題で易しめのやつ（むずい）
2020/02/20
ABC150 D- Semi Common Multiple
[最小公倍数、式変形]
本番通せなくて(c++わい、敗北）、Python勢がオーバーフロー？ｗ知らんけどｗｗｗｗｗｗ みたい感じになって俺がブチ切れたやつ。
2020/02/21
ABC067 D- Fennec VS. Snuke
[ゲーム、幅優先探索,queue,キュー,BFS,グラフ]
最適に動いたときどっちが勝つかってやつ。
第７回二本情報オリンピック予選(オンライン)
[ダイクストラ,クエリが与えられるタイプ,dijkstra,グラフ]
辺を追加するという操作か、二頂点間の最短距離を求めろ。っていうクエリが順次与えられる。 ダイクストラはある１点から他の頂点への距離の最短を求めるアルゴリズム。
2020/02/22
ABC 156 A-Beginner
[if文,日本語] Nが10以上の場合はRを出力, そうでない場合は内部レーティングを計算して出力する。
ABC 156 B-Digits
[K進数,whileループ] 10進数で表された整数Nは、K進数だと何桁で表せるか. ちょっとｳｯってなりましたけど、殴りました。
ABC 156 C-Rally
[全探索] 簡単. 考えるだけ無駄鳴きがする…（難しいのが出てきたらソノトキ考えよう)
ABC156 E- Roaming
[nCm,操作,組み合わせ、数え上げ、日本語]
本番通せなかった。けど頑張れば解けるような問題。
各部屋にいる人数だけが問題になっていて、中にいる人の違いは考慮しないってことに気が付かなかった。
2020/02/24
ABC104 D-We Love ABC
[動的計画法、数え上げ,mod]
青パフォで少しむずかしめの問題。ABCが何組あるか。みたいな…。 実質写経ACみたいな感じ。
ABC156 D- Bouquet
[mod,nCm,繰り返し二乗法、数え上げ]
可能な花束の作り方は 2n - 1 - nCa - nCb です。
AGC003 B- Simplified mahjong
[貪欲法]
簡単
ABC054 C- One-Stroke Path
[グラフ,無向グラフ,簡単グラフ,全順列]
2020/03/04
ABC157c Guess The Number
[全探索,if文ゴリ,実装ゲー,しんどい]
ABC157d Friend Suggestions
[UnionFind,ユニオンファインド,グラフ理論]
初めてunionfindをつかう問題だと本番で気づき、さらに通すことが出来た（やったね）
2020/03/11
この日の記事
セグ木をやった日です。
AOJなどをやっていたのでここには載せません
嘘です。載せます
AIZU ONLINE JUDGE Range Minimum Query
[SegmentTree,セグ木]
典型セグ木みたいな？
yosupo judge - Point Add Range Sum
[SegmentTree,セグ木]
初のヨスポジャッジからの記事です。
上の典型セグ木のコードを少し変えて頑張って解きました。
2020/03/12
yukicoder Range Mindex Query
[Seg-tree,セグ木,RMQ]
RMQのindexを答えてくれという問題です。
この問題を通して得た知見をつらつらと書き連ねていきます。
2020/03/13
ABC052C - Factors of Factorial
[全探索,約数の個数]
2020/03/16
ABC044 C-高橋くんとカード
[DP,3次元DP,動的計画法,水色パフォーマンス]
自力ACして糞盛り上がりました。
2020/03/20
ABC038 C-単調増加
[尺取り法]diff試験管900
愚直は通らない。通さない。
ABC115 D-Christmas
[再起関数,ムズカシイ]
むずくね？
写経AC
良うわからん
ABC075 C-Bridge
[橋、連結無向グラフ]
橋の問題です。他人の記事からうばってAC
この日の記事にちょっとだけ考察というかお気持ちというかが描いてあるかも
2020/03/21 AGC043の日
ABC075 C-Bridge
[橋、連結無向グラフ]
2020/03/22
ARC005 B- P-CASカードと高橋君
[天才実装ゲー,方向転換の処理]<br>
ABC159 A- The Number of Even
[偶数奇数,parity]
2つの数を足したら偶数になるような2つの数の選び方は、偶数+偶数か奇数+奇数ですよ。っていう問題.
ABC159 B - String Palindrome
[Palindrome,回文]
この問題面白くて、実はSが回文で、Sの前半も回文だったら、Sの後半調べなくていいんだよ。すごくね？
ABC159 C- Maximum Volume
[小数を使えますか,体積の最大化]
立方体が一番おっきいの！！
ABC159 D- Banned K
[map,連想配列]
ABC159 E- Dividing Chocolate
[bit全探索,天才実装]
ホワイトチョコレートと普通のチョコレートが混ざった板チョコなんて現実に存在しますか？しません。しません。しないで。
2020/03/24
ABC097 C- K-th Substring
[部分文字列,substr,連想配列,文字列,辞書順]
辞書順でK番目であるということについての考察。
"abcdef"と言う文字列sがあったとき、その末尾(プレフィックス)を取ったもの"abcde"文字列tは、sよりも辞書順で前か後か。どっちでしょうか。
ABC045 C- たくさんの数式
[bit全探索]
みんな大好きbit全探索の問題です。
ABC129 D-Lamp
[最大化,数え上げ的な]
diverta 2019 Programming Contest D- DivRem Number
[整数,約数,商と余り]
何か解けちゃいました。
2020/03/25
この日の記事
Indeedなう(予選B) B- 高橋くんと文字列操作
[文字列,文字列の比較]
2020/03/26
この日の記事
ABC124 D-Handstand
[尺取り法,累積和]
2020/03/27
この日の記事
AGC033 A- Darker and Darker
[複数ヶ所からの幅優先探索]
複数ヶ所からの幅優先探索というのは僕がみたときの印象です。
が、やってることは本当に基本の幅優先探索と一緒で、最初queueに突っ込むのを左上（0,0)だけじゃなくて
'#'のマスを全部queueに突っ込もうね。っていう考えです。
2020/03/28
ABC160 A-Coffee
[文字列,if文]
ABC160 B-Golden Coins
[切り捨て,最大化(easy)]
ABC160 C-Traveling Salesman Around Lake
[図形(?),最短距離(easy)]
池の周りのセールスマン
ABC160 D-Line++
[連想配列(map),無向グラフ(だけど…),最短距離]
無向グラフとか言われて身構えさせられたけど、辺を受け取る処理も書かなくていいので怯えるな！！って感じな気がした問題
ABC160 E-Red and Green Apples
[組み合わせ…？,最大化]
2020/03/29
この日の記事
ABC121 D- XOR World
[XOR,周期性,累積和的解法]
実は、kとk+1のXORは1かになる。(ただし、kが偶数のとき）(k = 3とすると3は011,4は100なのでXORは100で4ですね。進数変換は察して)
累積和的解法というのは、BまでのXORからA−1までのXORを引いてあげれば解けるっていうノリです。
僕は、1番目のbitが立っているのが何個あって…っていうのを求めて解きました。くそ汚い解法です.
2020/03/30
CODE FESTIVAL 2015 予選 A
[最適化,最小化]
公式解説PDF
公式のスライド解説って見やすくていいですよね。
- とりあえず全部を写すことにする
2020/03/31
記事に詳しく書いてあるわけじゃないのでこの日のブログのリンクは無し
ABC112 C- Pyramid
[重実装,全探索]
何か解説動画でウンウン言っていましたが，正直良くわからなかった．
解説PDFをみた感じで，一番わかり易い(それが知れたら解ける）のは，h[i] != 0 となるiが存在すること．これがわかれば解けた．
2020/04/01
ABC090 D- Remainder Reminder
[固定,数え上げ]
余りを求める問題は，余りに周期性があることを意識しよう。
つまり，0,1,2,...nをkで割った余りは0,1,...k-1, 0,1,...,k-1, ..., r
というふうに循環し，このときのrはn%kですね（そりゃそう)
2020/04/02
ABC080 C-Shopping Street
[bit全探索,条件,最大値]
最大値は負にもなりうるので，ans = 0;で初期化するのはダメだよ.
2020/04/03
ABC81 D- Coloring Dominoes
[数え上げ,mod,解説AC]
横ドミノが並んでるときに3倍じゃなくて2倍になると思ってた…
パターンを全通り考えよう！
2020/04/04
ABC161 A- ABC Swap
[特になし]
中身を入れ替えるという操作は2回しかしていないので単純にz,x,yの順に出力するだけですね
ABC161 B- Popular Vote
[割り算]
1WA出しちゃいました（ﾃﾍﾍﾟﾛ）
楽な実装方針ですと，a[i] * 4 * mが総得票数を上回っているか見たほうが楽そうですね。
総得票数 * (1/4m)とすると，切り上げれば良いのか切り捨てれば良いのか頭がﾎﾟｱになってしまうので，a[i] * 4 * m >= 総得票数をチェックしたほうが良いとおもいます。
もちろん大きい順に（降順）ソートしている前提ですよ。
ABC161 C- Replacing Integer
[数学,パターン]
何かよく分からない雑な考察とif文3つで通してしまいました。解説を読む必要があります。
なるほど，N,Kの大小で考察をすると楽だったのですね。
ABC161 D-Lunlun Number
[BFS]
既にlunlun数だとわかっている物を10倍して（追加できるなら）それ-1, +0, +1 をlunlun数に追加する。
解けた。楽しい。
2020/04/05
ABC105 C- Base -2 Number
この日の記事
[数学,-2進数,進数変換]
解けたけどよく分かってない。
ただ，なんとな〜くだけど，大事な（他の進数のときも意識したほうが良さそうな）ことは，k進数にするときは，kで割った余りがある条件になっていたらk進数のそこのフラグが立つ。で，その次のフラグを見るためには元の数をkで割って見る。って感じにするのが大事なんだと思う。
ABC109 D- Make Them Even
[操作，偶奇,最大化,貪欲法]
偶数と奇数しか見なくていいので，なんとなく右下に寄せていくイメージで行けば良さそう。
どのマスも必ず1回以下の操作をすれば偶数にすることが出来る。
だから，もしも奇数個のコインがあるのであれば右（右にマスがなければ下）に移動サせる。
右下のときだけどこにも移動させれないので偶数にならない可能性がある
2020/04/06
ABC138 D- Ki
[木，Tree,累積,深さ優先探索]
はい，出ましたAfter Contestのテストケースを乗り越えられなかった問題。
ポイントは木の持ち方,DFSのやり方(ってすぬけさんが言ってた）
2020/04/07
CODE FESTIVAL 2017 QUAL A C- Palindromic Matrix
[回文,文字列,手を動かせ]
手を動かしてみるとなんとなく見えてくることがあります。
2020/04/16
この日の記事
ABC162の回です
ABC162 A- Lucky7
[桁の値]
ABC 162 B- FizzBuzz Sum
[全探索,FizzBuzz]
Nの値が106までなので，全部見ればいいっすね。
ABC162 C- Sum of gcd of Tuples(EasY)
[全探索，最大公約数]
ABC162 D- RGB Triplets
[数え上げ,組み合わせ(?),条件]
中々面白い問題ですね。これが速く解けるか解くのに時間がかかるかで蒼perf ~ 緑perfまで変動するみたいです。にゃーん
とりあえず，RGBそれぞれの数を数えてあげましょう。
2020/04/22
この日の記事
ABC163の回です
ABC163 D- Sum of Large Numbers
[数え上げ]
unrated回なので考えずに終わってしまいました。N+1個の数は10100 + i と言う数で表されていて，
ある数h個取った時とg個(h!=g)取った時の値は絶対に一緒にならないので，取る数が何個かを全部見てやればよさそうです。
2020/04/27
ABC148 E- Double Factorial
[約数の個数,10進数]
N!!が10を約数に何個持つかっていう問題。
まずはNの階乗の中に何個2や5があるかっていうのを数えてみる。
1,2,3,...N(N個)の中に何個5の倍数があるか，それはN/5個だね。
これら5の倍数のものを全て5で割ると,
1,2,3,...N/5(N/5個)ってなっていく，これらを繰り返すことで，N!が5で何回割れるかっていうのが
求まる。
で，多分それが答え。
ちなみにNが奇数のときは，1,3,5,...,NがN!!で2が含まれることがないので答えは0
ABC148 F- Playing Tag on Tree
[木,鬼ごっこ]
高橋くんの初期位置からの距離(T)と，青木くんの初期位置からの距離(S)のうち，T < S となるようなSのうち最大のもの-1が答え（のはず)
二人の距離が偶数奇数によらず追いかけっ子が終わる場所が同じっていうのが面白いね
ABC158 E- Divisible Substring
[累積和,文字列中の整数,部分文字列,10進数]
15943 = 3 + 40 + 900 + 5000 + 10000 的なノリを10進数は大事にすると良い。
ってかこの問題すげえっすわ・・・
累積和を作ったときに(S) S7 ≡ S3 なら P で割れるだって！？まじか！すごいっす！みたいな。
2020/05/28
ABC106 C- To Infinity
[文字列、大きい数]
これはまああれですね。
あなたは2の5000乗が1018を超えるということに気が付きますか？
2020/05/29
ABC166 E- This Message Eill Self-Destruct in 5s
[連想配列,式変形]
・2人の持つ番号の差の絶対値が、2人の身長の和に等しい。
そのような(i,j)(i != j) の組を求めよ。という問題
つまり $a[i] + a[j] = |i-j|$ を満たすi,jの組を求める。
組み合わせを数えるから、(i,j)と(j,i)は同じ物として考える。
j > i となるような組だけ求めればいい。
先程の式を変形すると$a[j] + j = i - a[i]$となる。(iとjに着目して左辺と右辺に分ける)
つまり、各jに対して、a[j] + j が i - a[i] となるものを数えてあげればよくて、これを数える為にi < j となるiを全部見ることは愚かなので、連想配列に格納することで、a[j] + j = i - a[i] を満たすiをMAP[a[j] + j] を見るだけで数えられる！（やった〜！）
ABC070 D- Transit Tree Path
[木、DFS,深さ優先探索]
まぁ、深さでも幅優先探索でもどっちでもいいとは思うけど（知らん）
とりあえず求めるのは、Kが固定サれているっていうので、Kから各頂点への距離を最初に全部調べて上げればいい。 （与えられるグラフは木なので、Kから各頂点への距離はただ1つに定まる）
後はQ回のクエリで,1と8が与えられたら、1からKへの距離+Kから8への距離を答えとして出力する。
この問題、最近のABCで出たらdiffはどんなもんだろう…2017年8月の問題で、diffiが1190だけど、今でたら1050ぐらいまで下がるのかな？それとも茶パフォぐらいまで落ちるのかな？
個人的には深さ優先探索は書くのが苦手だから4桁diffあるような気がするけど...
ARC062 / ABC046 D- AtCodeerくんと変なじゃんけん
[貪欲？？]
これは何でしょうか…？
TopCodeer君がpを出した後、AtCoDeer君がpかgかをとりあえず考えてみた。
p-gで負けの時、ポイントは-1, その後1点にするためには2回勝たないと行けない…
（だからソレがどうした？？）みたいなよくわからないことを考えてみた結果、パーを出せるときはパーを出しておけ。みたいな考えになってとりあえず提出してみたラACした。
解説見ました。天才かよ・・・・・・・・・・・・・・・・・・・・・・・！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！
一回全部グー出したとして、どこをPに変えるかを考える…すげええ！！！！！！！！！
2020/05/30
[この日の記事]
ABC089 D- Practical Skill Test
[累積和,コスト,割った余り]
LとRが与えられた時、L -> R のコストは L % D を K とした時（ただし,K = 0のときはK = Dとする), K -> R のコストから K -> L のコストを引いたものとして求められる。
(A -> B -> C という経路があれば、BとCの距離はAとCの距離引くAとBの距離的な）
SoundHound Inc Programming Contest2018 C- Ordinary Beauty
[期待値の線形性]
なんや難しそうな問題だなぁ…
隣り合う二項について美しさを獲得できるかどうかで求めていけないかな…うんぬん…とかしていて結局解けないことが分かりました。
解説PDFを見て1mm理解,その後、数学/競プロメモこの方の記事を読んで1cm位理解しました。 なるほど。まぁ、二項間について着目しようという発想はヨカッタですね。各2項間について、得られる美しさの期待値を求める。他の2項間についても、美しさを得られる期待値は同じなので、存在する二項間がm-1個あるから、各二項間の美しさの期待値 * (m-1)が答え。ふうん。面白いじゃん。 期待値の線形性ね。なるほど。
NOMURA プログラミングコンテスト2020 C- Folia
[二分木,木の構築?,葉の数]
2020/05/31
ABC169-A Multiplication 1
[yarudake]
ABC169-B Multiplication 2
[いじめ,オーバーフロー]
1e18を超えた時の判定がむずいので
$ now * a[i] > 1e18 $ ってことは
$ now > 1e18 / a[i] $(式変形)かぁ、って思ってそうしたら行けた。
ABC169-C Multiplication 3
[いじめ,オーバーフロー,小数]
ABC169-D Div Game
[素因数]
$ N = a ^ x * b ^ y * c ^ z $みたいな形してるとき、xを1+2+3+...+kって感じで分割するのが良くて…みたいな感じでやってったら行けた。
ABC169-E Count Median
[中央値,最大化,最小化]
何も分かっていないので解説動画を見よう！！！
2020/06/01
ABC 096 D- Five, Five Everywhere
[面白い,素数,合成数]
解説ACなのですが、感動しました。
{x1, x2, x3, x4, x5} のxiがそれぞれ5 * k + a (aが5で割った余り)という形で表されるとき x1 ~ x5 までの和は 5 * hoge + 5 * a なので5の倍数だね！！ﾌﾌﾝ
ABC092 C- 2D Plane 2N Points
[ペア作成、貪欲(的),最適な選び方]
こういう問題よくあるよね。好きだよ。好きだよ。
あれです、クイズ番組で10人が問題を解く。難易度は1〜10までで10個ある。って時、自分が解けるなかで一番難しい物解いてあげよう。っていうやつだよ。
AGC024 B- BAckfront
[操作の最小回数,数列並び替え]
?2?3??4??5? みたいになっている時、（この文字列は9文字)2345以外の?に操作を加えることで 1 2345 6789っていう風にすることが出来る。!!!!つまり、与えられた数列の中で、 k (k+1) (k+2) (k+m) っていう順に並んでいるモノの最大値を求めて上げればいいって。
2020/06/02
AGC 032 B- Balanced Neigbors
[グラフ,グラフの構築]
解けなかったけど、なんかグラフ関連の問題なんてまだ累計50問も解いてないだろうし、そもそも考える方法が分かっていないみたいな節ある。
ただ、今回の問題だと完全グラフをまず構築してみる。とかそういう物を頂いたので収穫はありかと思われます！！！
完全グラフ(頂点i,j(i != j) の2頂点について、どのi,jの組み合わせも辺がある)を考えて、その時の各頂点の隣接している頂点の和を見てみる（(1~Nの和) - (見ている頂点番号)) 。 そこから考えていくととても良い！！ へーかっけえ おれもこんな問題が解ける天才になりてえな
ABC097 D- Equals
[UnionFind, 連結,好きな回数操作]
a <-> b <-> cって感じでaとbの入れ替え、bとcの入れ替えが出来るなら、abcの順列(abc, acb, bac, bca, cab, cba)はどれでも作ることが出来る。
つまり、(1 <= k <= n) の k が最初入っていた場所と、kが本来ある場所が関節的にでも繋がっていればkは目的の場所へ移動することが出来る。
自力AC,やったぜ。
連結なら全部目的の場所に行ける、っていうのは、なんかまぁ、バブルソートでどんな数列でも昇順に出来るし、見たいなノリで考えるとタシカニな〜みたいなうっすらとした感覚がある。
(この、swap操作って、バブルソートみたいなもんじゃね（Sirankedo)
M-SOLUTIONS プロコンオープン D- Maximum Sum of Minimum
葉には一番小さい要素を入れる。というふうにしてみたのですが駄目でした。解説ACでぷ。 深さ優先探索を書いてみようと思ったらバグ梅小宮で解けなかったのでおとなしく幅優先探索を。
この問題名でググると他の方の解説記事あって、それとても良いと思ったから俺の記事なんか読むよりそっち見てみて。
c1 >= c2 >= ... >= cn とすると、ci( 1 <= i <= n) は最大でも(i-1)回しか足せない。
ってことが分かるので、 可能かどうかは分からないが、最大でも c2+...+cn が答え。（まぁ、可能)
どっかを木の根として、根から幅優先探索でも深さ優先探索でも良いが、Cの大きいものから入れて行くと良いとのこと。
ちなみに解説の森が云々っていうのはわからんかった(元気もりもり森鴎外なら知ってる)
CODE FESTIVAL 2017 Final
[時計,円,場合分け,実装重い,bit全探索(的な)]
s = 0 〜12としたときに、達成出来るかで全探索しようと思ってpriority_queueを使って実装したのですが9WA出して諦めました。（なんだろう、こういう時原因を突き詰めるまでやったほうが良いとは思うが体力が)
2020/06/03
ABC137 D- Summer Vacation
[優先度付きキュー,(貪欲法)]
解説を見て、あぁ、M-1日目から順に考えていくのか…ってなったよね。
以下解説PDFより引用
こういった問題は、制約の厳しい方から見ていくと見通しが良くなることが多いです。 したい操作は
- 候補の追加
- 候補の中から最大のものを取り出す
にゃあ. 0日目に受けれる仕事は多い。M-1日目に受けれる仕事は少ない（日数の制約上受けれる（というか受けれるっちゃどれも受けれるが、報酬が間に合わない))ので制約がきびしい
AGC024 C- Sequence Growing Easy
[操作,数列]
(もはやタグ付がテキトウ)
当日の記事に、頭の流れ書いた。
2020/06/05
AGC031 B- Reversi
- [数列の操作,オセロ,数え上げ]
頭パンクしちゃうのでパス。
ABC114 D- 756
- [約数の個数,数え上げ]
約数の個数が75個って言うのはどういうことかって言うと、 75 = 3 * 5 * 5であることを考えて, (x,y,z) = (74,0,0),(24,2,0),(14,4,0),(4,4,2) の4つが考えられる…。
(14,4,0)の時を取り上げて、 k = a14 * b4 と表せるとき、kの約数の個数は75個だな〜…
このとき、aとしてかんがえられるものが何通りあるか、っていうのと、bとしてかんがえられるものが何通りあるか、って言うのをかんがえてあげれば、 a ^ 14 * b ^4 で表せる数っていうのは a * (b - 1)通りあるな。
あと、これは俺が間違えたことなんだけど, a * (b - 1) と b * (a - 1)はチガウから注意しようね。
エイシング プログラミングコンテスト2019
- [幅優先探索,交互に移動]
b2からw1は行けるのに、b2からw2,w3,w4へは行けないのがありえない。っていうのはどうやって示そう。
数学の素養が虚無だからテキトウなこと言うけど、 b2からw1へ行けたってことは、w1からb1へ行くことが可能じゃん。すると,b1からw1,w2,w3,w4へ行けるんだから、一回b1を経由して上げればw2,w3,w4へ行けるってことは理解できそう。
で、幅優先探索で行ける島を見つけてあげて、島に含まれるblackとwhiteの数の積を答えに足す。っていうのをやってあげれば答えが求まる。
僕はこれに バグを埋め込んで一生泣いてた。
diverta2019 Programming Contest2 C- Seccessive Subtraction
- [数列の操作]
(天才が)考察をすると,N個の要素について、最低でも1つは+と-があって、他のものについては+にも-にも出来ると言う事が分かります。
そして、肝心な操作の順番ですが、 イメージとしては、+にしたいやつは(aをのぞいて)2回 x,y のyとして選ぶことで正に戻す。みたいな感じかな。。
2020/06/06
AGC019 B - Reverse and Compare
-[数え上げ,要素の反転]
"aabbb"みたいなのがあったら、どの'a'をどの'b'と交換するか。みたいなことを考えるだけだと思いますが。
だから、'a'~'z'についてそれをやるだけですね。
'a'と'b','a'と'c',...,'a'と'z'次は'b'と'c', 'b'と'd', ... , 'b'と'z'って感じで、ね。
ABC055 / ARC069 D- Managerie
-[嘘つきと正直者,構築?]
Menagerieという英単語は、動物園という意味だそうです。
2匹を決めてやると、その後2匹目がSheepで発言が'o'なら、3匹目は1匹目と同じ動物。というふうに決めていくことが出来る。
1,2番目の動物の決め方は {wolf/Sheep} {wolf/wolf}, {Sheep,wolf}{Sheep,Sheep}の4通りしか無いので、4つの場合について、動物を決めていって、証言に嘘がないかを見てやれば良い。
似たような問題がbit全探索する問題であったような気がするな〜(ちょうどブログサボってた時期に解いたかも)
ARC062 C- AtCoDeerくんと選挙速報
- [最小化,DP,数式変形]
面白い問題ですね（解けなかったけど)
解説ACです。
まず、一番最初の速報の段階でx:yのとき、票はx,y票が最小ということは分かる。
次に、得票数の比がT:A(問題文と文字を合わせた）のとき、得票数はT * x[i], A * x[i]であるとします。
ってやっていくのであれば、x[n-1]を最小化してあげれば得票数も最小になります。
これをなんか美味いこと数式作ってやると解ける！すげ〜！
ABC152 E-Flatten
- [LCM,素因数分解、オーバーフロー]
全てのiについてAi * Bi をLCMにしたらいいってのは分かる気がします。
しかし、LCMを頑張って求めるとオーバーフロー！！ｱｱｱｱｱｱｱｱｱｱ！！！ってなりますね。
（本番なりました）
そこで、LCMを求めるのではなく、LCMを素因数分解した形を持ってやるという発想です。
賢いですね。そうすればうまく行く。
ABC099 D-Good Grid
- [MOD3,最小値,計算量削減]
とりあえず、問題の意図としては、使う色は3色だけになるぽよってことが分かりました。
じゃ,(i+j)%3が0,1,2で何色を塗るか30 * 29 * 28 通り全部試すか…ってやろうとするとO(N2 C3)で109ぐらいで許してくれません。（意地悪)
で、かんがえを変えて、とりえずMOD3が0,1,2のものそれぞれについて、色i( 1 <= i <= C)にした時の違和感を保持しておきます。
すると、MOD3が0のもの、1のもの、2のもので、違和感が小さい順にしたものを3つずつ取ってきて上げると、33=27通りのうち、どれかは採用出来るようになっています。
で、採用出来るかどうかを見てあげて最小値取ってあげる。
2020/06/07
ABC128 D- equeue
- [全探索(的な?),最大化]
この問題のポイントは以下に挙げる100000007つです。
- 操作の回数はK回以下
- 宝石を筒に戻す操作は最後に行えば良い。
- 左からと右から、何個ずつ取り出すかで場合分け.
1のK回以下という制約によって、右から取り出して右に入れて右から取り出して右に入れる。という操作(4回)を、右から取り出した後、戻すという2回の操作に出来ます。
ABC134 E- Sequence Decomposing
- [deque,最小化,LIS,LDS]
なんですかこれ、難しい。なんとなく、要素を左から見ていって、見ている要素を何と同じ色にするか、ってとき、出来るだけ大きい数字のものと一緒にすればいいっていうのは分かった。
ABC138 E- Strings of Impurity
- [部分列,超巨大文字列, 二分探索,]
うーん、なんとも…
超巨大文字列s'の何文字目を使うかっていうのを保持するのではなくて、sの何文字目を使うかでやっていくらしい。
そのためにsを2つくっつけたもので見ていくと。
解説シャキョウACだけどちょっと理解は進んだよ。
あ〜少しずつ分かってきた。面白い問題だね。k
Tenka1 Programmer Beginner Contest
- [構築,数式イジイジ,楽しい日曜日]
以下考察。
1~Nは、どれもちょうど2つの集合に含まれるということから、1が2個、2が2個…Nが2個ということで、S1からSnまでに含まれる要素の個数は全部で2 * N 個有りますね。
次に、構築する集合がk個の時、S1~Skのk個の集合を構築してあげます。
ここで次に、もう一つの条件を見ます。
S 1 , S 2 , . . . , S k のうちどの 2 つの集合をとっても、それらに共通して含まれる要素はちょうど 1 つである 。つまり、S1はS2と共通してa1を共通して持つ、S1はS3と共通してa2を持つ…S1はSkと共通してa(k-1)を持つ。という風になります。
よって、S1は要素を(k-1)個もちます。 他の集合S2~Skに対しても同様のことが言えるのでS1,S2,...,Skは全て(k-1)個の要素をもちます。
そして、S1からSkがそれぞれ(k-1)個の要素を持つ時、
S1の要素の個数 + S2の要素の個数 + ... + Skの要素の個数 = k * (k-1)
これが2 * N と一致していれば、そのような集合は作れます（証明:AC)
CODE FESTIVAL 2017 Final A-AKIBA
- [if文]
分からんかったので力で通しました。
int main() { string s; cin >> s; if(s=="AKIHBR") cout << "YES" << endl; else if(s=="KIHABR") cout << "YES" << endl; else if(s=="AKIHABR") cout << "YES" << endl; else if(s=="KIHBAR") cout << "YES" << endl; else if(s=="AKIHBAR") cout << "YES" << endl; else if(s=="KIHABAR") cout << "YES" << endl; else if(s=="AKIHABAR") cout << "YES" << endl; else if(s=="KIHBRA") cout << "YES" << endl; else if(s=="AKIHBRA") cout << "YES" << endl; else if(s=="KIHABRA") cout << "YES" << endl; else if(s=="AKIHABRA") cout << "YES" << endl; else if(s=="KIHBARA") cout << "YES" << endl; else if(s=="AKIHBARA") cout << "YES" << endl; else if(s=="KIHABARA") cout << "YES" << endl; else if(s=="AKIHABARA") cout << "YES" << endl; else if(s=="KIHBR") cout << "YES" << endl; else cout << "NO" << endl; }
2020/06/08
AGC039 B-Graph Partition
- [ワーシャルフロイド法,二部グラフ判定,グラフの直径]
各辺が隣り合う番号の頂点を結んでいるようにする。 各集合がNo Empty
どういうときに出来るか。二部グラフじゃないと駄目なことが分かる。全部の辺が偶数グループと奇数グループを結んでいるはず。
二部グラフではないとき、どう頑張っても全ての辺にたいして隣り合う頂点集合の頂点同士を結ぶことは出来ない。
二部グラフであるとき、二色で（白と黒)分けたものの、白から見て其の隣の黒を2,其の隣（最初の白じゃないやつ）を3…としていけば条件を満たすグラフは作れる。
うーん。なぜ二部グラフなら作れるのか。って言うのを理解するのが難しい‥けど。
頂点集合の数を最大っていうのを無視する。
すると、白を集合番号0、黒を1としてしまえば、全ての辺に対して、頂点番号k,k+1を結んでいる。というのは作れる。
この時、二部グラフだから黒同士を結んでいる（白同士を結んでいる）辺は存在しないので条件は満たしている（最大値は知らない）
ABC100 D-Patisserie ABC
- [BIT全探索,価値の最大化]
テキトウに、M個選んだ時の綺麗さの和,おいしさの和,人気度の和をX,Y,Zとでもしておきましょう.
このとき、(X、つまり綺麗さの合計の絶対値) + (Y,つまりおいしさの合計の絶対値) + (Z,い人気度の合計の絶対値) = S とでも置いておきます。
すると、S = +-(X) +-(Y) +-(Z) ですね。+-はプラスかマイナスかのどちらか。的なニュアンスで。
となると、X,Y,Z,それぞれについて正に大きくするのを目指す。負に大きくするのを目指すかでわけでかんがえると良さそうだな…って気がします。
ABC047 D- 高橋君と見えざる手
- [コストの最小化,差の更新,差の最大]
i番目の町まで見た時、i-1番目の町までで一番安い物を売ることを考える。
(2番目に安いものを売るよりも、一番安いものを売ったほうが利益が大きいから)
そして、i-1番目の町までで買ったりんごをi番目の町で売った時の利益がiまで見たときに最大なら、其の個数を管理する。
ABC059 C-Sequence
- [二通り試す,操作の最小回数]
なるほどね。i番目までの和が偶数のときと奇数の時を二通り試すのか〜…
0番目までの和はいじらなくていいだろ。って無意識に思ってました。
ABC120 D- Decayed Bridges
- [UnionFind,逆からみる]
M番目の橋から順に見ていきます。
まず、M番目の橋をつなげたことで、A[M]とB[M]が行き来出来るようになります。
逆にこの橋がなくなることで,A[M]とB[M]が行き来出来ないようになります。
この時増える不便さは1(A[M]とB[M]の一組だけ行き来できなくなるので.)
この、値"1"を heru という配列の0番目に格納します。
次にM-1番目の橋を見ます。
この時、M-1番目の橋を繋げたことで、何組の島が新しく行き来可能になったかを見ます。
この値を heru という配列の1番目に格納します。
これを1番目の橋までやっていきます。
heru という配列を逆順にします。
M回出力します。i回目の出力は、heruの0からiまでの値の和。
2020/06/09
AGC020 B- Ice Rink Game
- [後ろから,最大と最小,操作]
a[i]人組を作る操作で、人数はa[i]倍数人になる。
a[i]人組を作る操作で,N人組になるとき、操作の前では(N/a[i]) * a[i] 人かな？
ﾁｮｯﾄﾑｽﾞｶｼｲ(解説AC)
何書けばいいか分からないくらいにはわからないな。
ABC080 D- Recording
- [実装,同じチャンネルはお得]
時刻1~100010ぐらいまでについて、テレビが始まる時間と終わる時間を保持、終わった瞬間同じchで別番組が始まる場合はソレも保持。
ABC106 D- AtCoder Express 2
- [二次元累積和]
始めて二次元累積和の問題触りました。
良い言葉を書くには理解が浅すぎる。
ABC126 E- 1 or 2
- [UnionFind,Disjoint-Set,コストの最小化,数式]
A2 + A4 ≡ 0(mod2)って言われたら、A2が分かればA4も決まります。A4が分かればA2も分かります。
A4 + A5 ≡ 1(mod2)って言われていたら、さっきの手順でA2,A4が分かっているのでA5も分かります。
ABC153 F- Silver Fox vs Monster
- [疑似累積和,区間に対する操作,queue]
i体目にギリギリ届くように落とした爆弾の効果が、i+何体目まで及ぶか。っていうのをqueueで扱えるようにしたのですね。
while(q.front().first < x)
っていう書き方賢いですね。(q.front().firstは、効果が切れる時の座標、xは今見てるモンスターの座標)
AGC023 B- Find Symmetried
- [計算量減らせ,線対称]
A,Bで成り立つ時,A+1,B+1についても成り立つ！！！！
(A,B)->(A+1,B+1)は全部右下（イメージ)に1個ずつずらすだけなので、対象であるかどうかには影響しない！！！
だからA=5, B=6 をみる変わりにA=0,B=1を見れば良い。（A=0とB=0~N-1を見てやればいい！！）
2020/06/10
ABC033 B- LRUD Game
- [場合分け、勝てる区間]
駒が盤面から落ちる場合、右から落ちるのか、左に落ちるのか。上から落ちるのか、下から落ちるのか。この4通りを見てやるのが僕的には楽だと思います。
解説動画だと、勝てる区間？とやらがあるみたいですが、そちらについては理解が追いつきませんでした。
第5回 ドワンゴからの挑戦状 予選
- [桁ごとにみる,実装,for文はまとめろ]
2k > 2k-1 + 2k-2 + ... + 20
めちゃくちゃ時間かかった
ツカレタ。
240ぐらいから,そいつを採用出来るか見ていく（部分列の和の最大は,a[0] ~ a[n-1]の和、すなわち109 * 103 で1012 ≒ 240ぐらいなので)
ABC131 E- Friendships
- [グラフの構築,構築ゲー]
構築ゲーは、極端な例ヲかんがえてやると良いらしい。 作れる上限と下限を考える。
2020/06/12
AGC041 B- Voting Judges
- [二分探索、単調性,実装頑張れ,二分探索の端っこ]
ng = n + 1;
これはWA
ng = n;
これはAC。
…難しいよ…
写経ACじゃないので自力ACと言っても過言ではない。
まず、得点5が採用できるなら、得点5以上は全部採用できる。
得点4は採用できるか分からない。
つまり、得点Kが採用可能なとき、K以上は全部採用出来るから、其のようなKの下限を求めろっていう、二分探索が使える。
A[i]が採用可能かを判定してあげる。
A[i]がｷﾞﾘｷﾞﾘ採用できる〜〜って時をかんがえて挙げると、P位にてあげればいい。そうするとき、どうやって票を振り分けて行くかを考えればOK !!
ABC165 D- Floor Function
- [床関数,数式,最大値、周期、割った余り]
単調増加関数、周期がB,,,....
まぁまず、xの値をNまで全探索するのはO(N)で N <= 1012なので無理。
式の値がBで周期になってるってこと、気づくの無理じゃね…？(代入しないで式で気づくの無理そう) 周期がBってことに気付ければB-1の時一番嬉しいって分かるな
2020/06/13
ARC074 C- Chocolate Bar
- [面積、差の最小化]
二週間前に解こうとして、解けなくて投げ出した問題をちゃんとACしました（やった〜)
線の入れ方は、{横に引くのを二本,縦に引くのを二本,横と縦1本ずつ}
の3通り。(と見せかけて、縦横一本ずつは少しチガウ)
AtCoder Beginner Contest 079 C- Train Ticket
- [全探索,(bit全探索)]
8通り全部ifで書くのがめんどくさいのでbit全探索しました。
2020/06/14,15
ABC170 E- Smart Infants
multisetから、ある値xを一個だけ消したい時は,s.erase(s.find(x)) 配列の要素の先頭の値は(配列の名前をsとすると） Editorial - NOMURA Programming Contest 2022（AtCoder Beginner Contest 253）
*(s.begin())
末尾の要素は
*(s.rbegin())
で取得出来る。
Codeforces Round #599(Div.2) A.Maximum Square
- [全探索]
辺の長さ1 ~ 1000が作れるか全部見てあげても間に合う。全体の計算量はO(KN2) <= 107かな 各辺の長さLについて、N枚の板がL以上かを見る。その枚数がL以上なら辺Lは作れる。
Codeforces Round #599 (Div. 2) B2. Character Swap(Hard Versiion
- [操作、整列]
操作が2n回まで出来るってことは、ある文字を希望通りの位置に持ってくることは出来る。
Codeforces Round #599 (Div. 2) C. Tile Painting
- [割った余り？,実験,最大化]
Nが素因数一種類で構成されているならその素因数が答え。(N = 39なら3が答え)
Nが2種類以上の素数で構成されているなら答えは1
(記事に落書きあり)
2020/06/16,17
東京海上日動プログラミングコンテスト
C. Lamps
- [操作回数の最大]
最大でも50回ぐらい操作をすれば値は収束する。（僕は1000回ぐらい回せばええやろっていってTLEでした。うざい)
Codeforces Round #514 (Div. 2) A.Cashier
- [切り捨て]
客が返ってから次の客がくるまでの時間(最後に客が来る時間をL(一日の長さ)としておくと都合がいい) で、何回休憩が取れるかを取っていく。
Codeforces Round #514 (Div. 2) B.
ポチになる可能性があるのは、外周をぐるっとする1マスの枠より内側にあるので、ソレを全部ポチとして採用するか見てやる。
Codeforces Round #514 (Div. 2) C.
- [落とし込み,約数,最大公約数,場合分け]
最初取る最大公約数は絶対1って言うのは分かる。
じゃあ、出来るだけ早い段階でGCDが2以上となるようにしたい。
サンプルを見てみると、N = 3 のときは、3がGCDとして取れるようになってる。
まぁなんか、早くGCD大きくしたいよ〜ってとき、最低でも要素数/2 ぐらいすればGCD大きく出来るよ。的な。
ABC170 D- Not Divisible
- [素数っぽいやつ,エラトステネスの篩っぽいやつ]
まず入力を昇順に並び替えとく。
2が与えられたら,4,6,8,...は以後出てきても答えに加算はされない。みたいなエラトステネスの篩っぽいことをして素数っぽいやつの数を数えればいい。解けた時自分が天才かと思った。
ABC157 E-Simple String Queries
- [set,集合を管理する,query,アルファベット]
'a' ~ 'z'の26文字についてを管理する。
'a'なら'a'が何文字目にあるかを保持。このように'a'のある位置を管理する配列~'z'のある位置を管理する配列を用意する。
文字の置き換えqueryに対しては、置き換わる前の文字列が何かを見て、其の文字の集合から、其の文字の位置を削除。（S自体も置き換える)
新しい文字cに対して、cが何番目にあるかを管理している配列に対して、追加する。
範囲queryに対しては、'a'~'z'があるかを1文字ずつ判定
これは、setの中身に対してLi文字目以降ではじめてc( 'a' ~ 'z'がc)が出てくる場所を見つける。見つけた位置がRより手前なら（Li以降で見つけているので)文字cがある。
今度似たような問題が出たら自分で解きてえ
ABC141 E- Who Says a Pun?
- [文字列,DP,後ろからDP,Z-Algorithm]
dp[i][j] := i からと j から始めたときに一致する最大の長さ
DPを使うことによって、i文字目から見たsubstringとj文字目から見たsubstringについて、何文字共通するかを全てのi,jの組についてO(N2)で求めることが出来る。
EDPC F-LCS
- [DPの復元,DP,最長共通部分列問題,部分列]
最長の長さを取ることは出来たんだけど、DPの復元が分からなかった。
けんちょんさんの記事読んだんだけど、そのDPの値がどこから来たのかっていうのを考えるとわかりやすかった。
EDPC G- Longest Path
- [DP,有向グラフ,再帰関数,トポロジカルソート]
DPの表って、出来ているものから出来ていないものを作っていくイメージだったんだけど、今回のような、（僕の中のイメージで）葉から根に向かって値を作っていく（根が呼び出しのもと)ようなときには、再帰関数を使えば逆から埋めていけるようだ！！（久しぶりに再帰書いた（書いてない））
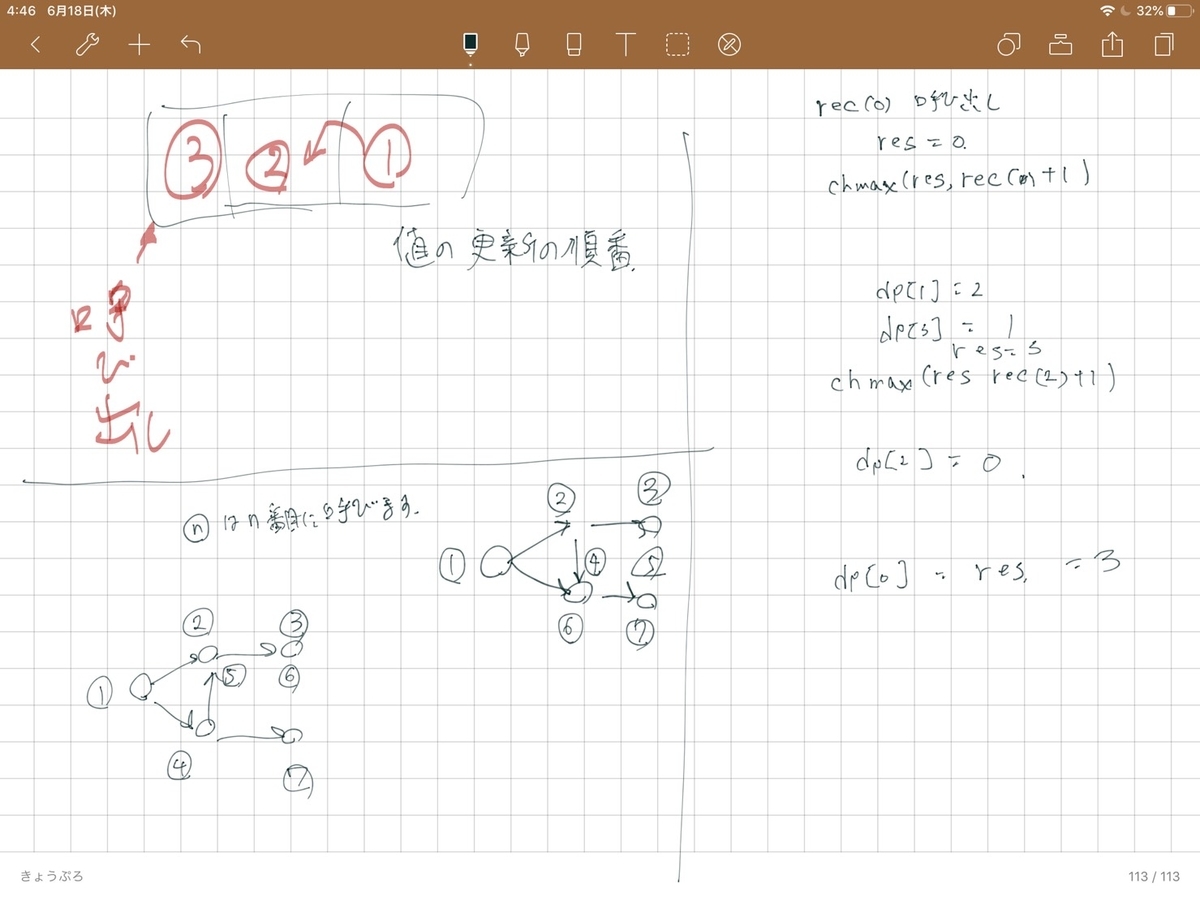
2020/06/18
EDPC H- Grid 1
- [DP,迷路,幅優先探索]
僕が解けるDPだ、ありがたいですね。
あるマスが通過可能なマスの時、其のマスへ行く方法は、左のマスから行くか、上のマス(まぁ、どこを上と見るかは人によると思うけど)から行くかの二通りしか無い。
この時、左のマスへ行く方法がL通り、上のマスへ行く方法がU通りあるなら、其のマスへ行く方法はL+U通りだなあ。ってやつ。
初期条件として、(1,1) へ行く方法が1通りだというのさえ知っていれば解ける。
EDPC I- Coins
- [確率DP]
解けた〜！！（やった〜）
小数が出てくるから確率大っ嫌いなんですけど、doubleで通ったのでよしです。
僕は１次元dpで解きました。
表がN枚出る確率 -> 表がN-1枚出る確率 -> ... -> 表が0枚出る確率
という順番で後ろから更新しました。
i枚目のコインについて見ている時,表がK枚出る確率は、K-1枚表が出る確率 * i枚目が表 + K枚表 * i枚目が裏
事故らないようにDPしてるので事故りません.
EDPC J-Sushi
- [期待値DP]
０枚の皿の数、1枚の皿の数の枚数、2枚の皿の枚数が重要そうだなっていうところまではなんとなく思いました。
漸化式の部分が完全な理解とはほど遠いですね。
CODE FESTIVAL 2016 qual C
- [矛盾判定,何通り]
二人の証言から、山の高さが確定したタイミングというのをかんがえました。
まず、0番目の山の高さはt[0]であることは分かります。
(t[0] := (0~0)番目までの山の中で最大の高さ。 )
同様に、n-1番目野山の高さはa[n-1]であることも分かります。
(a[n-1] := (n-1 ~ n-1)番目までの山の中で最大の高さ)
2020/06/19
AGC002 C-Knot Puzzle
- [天才パズル,未証明貪欲,dequeではない,達成可否]
この問題、dequeで端から小さい方を取る。みたいな感じでやると死にます。
L = 8
3 5 2 4 4 1
をかんがえて
小さい方から取ると L(left) RRR となって、5,2が残ります。すると、もうほどけません。
でも、4 4 を残してやればほどけます。
これがdequeでやった時死ぬコード。
では、どうすれば良かったか、
それは、 a[i] + a[i+1] の最大となる二点を残して上げるのが一番良いです。
これがL以上であれば、絶対に達成出来ます。
ABC075 D-Axis-Parallel Rectangle
- [五重ループ,点を含む個数,二次元累積和っぽさ]
AtCoderExpress2この問題にニているものを感じたが、制約で二次元累積和出来ない…ってなった。
解説を見ると、二次元累積和が使えるらしい。(まじか)
採用する長方形の xの左端、右端,yの上端下端を全探索(候補はそれぞれ点の数だけ)。賢いなああああああ・・・・
AGC003 C-BBuBBBlesort!
- [天才パズル,偶奇,操作の最小化]
何回要素の反転行っても良いんだって。
まず、Aの偶数番目の要素を取り出して考えると、これは操作2だけで任意の順番に並び替えることが出来ます。
3つの順番を反転とあるが、1つ目と3つ目だけに着目すると、ただこの2つの要素が入れ替わっているだけなため、偶数番目の要素が2つswapされるだけです。
数列はswap操作だけでソート出来るので、偶数番目だけを昇順に並び替えることは操作1を一回も行わずに行うことが出来ます。
奇数番目も同様です。
ABC144 E-Gluttony
- [二分探索のプロ,内積の最小化]
伝家の宝刀二分探索!!! a[i] * f[i] をある値に出来るかを計算するコストはO(N)。 a[i] * f[i] であり得る値は最大でも1012 、log(1012) は40ぐらい、これなら行けるぞ。
まず、前提として、数列aとfがあって、a[i] * f[i] の最大を最小にしようってしたとき、aは昇順、fは降順（逆でもいい）っていうのは使えそうだ。
ちなみにこれは、a[i]に修行させた時、減るコストはf[i]なので、f[i]が大きいものに大して修行させたときのありがたみがでかいよね。的なかんがえ（あとで解説読む)
それで、a[i] * f[i] の最大値をMに出来るかっていう時、其の判定をどうするかをかんがえます
各iについてa[i] * f[i] = Mにするための修行回数を数えます。
このとき、(iの修行した後の消化コスト) * f[i] が Mを下回るとき、其の値はMを下回る（＝もおっけ)最大のf[i]の倍数です。
よって、iが修行する回数は max(0,a[i] - M / f[i])として求められます。
例えば、a[i] = 3, f[i] = 9 のとき、M = 15を目指すとすると、 修行する回数はmax(0, ai - M(15) / fi) = max(0, 3-1) = max(0,2) = 2となって、二回修行すればいい。
これをN人全員見てあげて、必要な修行回数がK以下だったら、Mは達成可能ということになります。
よって、Mが達成可能化はO(N)で判別出来ることが分かりました（やったね)
CODE FESTIVAL 2016 Final C-Interpretation
[通訳,UnionFind,集合の管理]
各i人目について,Ki個の言語Li1,Li2, ... , LiKiをユニオンファインドで合併する.
- 0人目が話せる言語をXとする
- 各i人について、iが話せる言語を一つ持ってきて、Xとiが同じ集合にあれば,とりあえずok
- Xとiが同じ集合になければNOを出力して終わり。
- とりあえずokがN人全員について言えたらYES
ARC090 D- People on a Line
- [写経AC,有向重み付きグラフ,矛盾判定]
難しいですね。(何をコメントしたらいいかわからない)
とりあえず、数式で繋がっている頂点（人の位置)は相互に関係しているので、一つ決めた時もう一つも決まる。そこから派生してもう一つも決まる。みたいなのはグラフで管理していけばいいみたいです。
A - B間の距離が3の時,Aから右に3行けばB、とともに、Bから左に3行けばA、っていう辺を2つ作ります。
これでうまく行くっぽいです、難しいですね。
とりあえず人の写経コード貼っときます（こら)
ABC040 C-柱柱柱柱柱
- [動的計画法]
動的計画法の初級っぽい問題(バグらせたけど)
i本目の柱へ行くコストを最小化しながら更新していけばいい。
綺麗なコードが書きたいな
ABC036 C-座圧
- [ソート,連想配列]
実装頑張れの問題。
まず、aを昇順に整列したものが手に入れば、各値をどうしたいかが分かる。aを整列したとき一番小さいものが0,2番目が1ってなる。
よって、各値が何になってほしいかを連想配列で管理してやれば良い。
ABC035 C-オセロ
- [優先度付きqueue,ノリと根性]
L~Rの区間をヒックリ返しますよ〜ってとき、何回ひっくり返している。っていうのを保持しておいて、で、Rを過ぎたら其の回数を減らす。。。みたいなことを… Lが来るたびに何回ひっくり返してるかを+1して、Rをすぎるたびに-1する。
爆弾でモンスター倒すやつ。みたいな考え方を使って解きました。
あ、これ、配列でも解けるな。
気合で。
あ、これ配列使ってやるのいもす法って言うらしい。（ってかそもそもpriority_queueも配列を使っているのでは)
ちょっと実装してみるか.
ABC030 C-飛行機乗り
- [うなぎってなんだよ,priority_queue]
N,Mが105程度なので、2 * 105 回、それぞれ採用するかどうか見るぐらいなら余裕で間に合います。
どれぐらい余裕かって言うと、生まれたての子鹿を片手で捻り潰すぐらいには余裕です（こら)
飛行機に乗っている時間っていうのは短いので、乗れるなら速いうちに乗ったほうが良いよね。
だから、空港Aから乗れる一番速いのに乗る,空港Bにつく。Bから乗れる速いのに乗る。
(速いじゃなくて早いなんだけどね)
っていうのを実装してやれば行けるね。
2020/06/20
ABC022 C- Blue Bird
- [天才パズル,ワーシャルフロイド法,全点対間最短距離,閉路から経路]
想定解法が賢すぎる。
閉路に対して、ある頂点を1個除いてやれば、辺の数が2個減った経路になる。
ABC021 C- 正直者の高橋くん
- [BFS,最短経路,経路の数え上げ]
ミスったこと、1e9+7で割った余りを出力するのを忘れていた
- 難しかったこと
BFSのときに、既にみた頂点とか、そこに行く道の最短であるよってことをどうやって書くかに悩んだ。
Aからの距離がKの頂点xに行く最短の道順が何通りあるか。
それは、Aからの距離がK-1であり、さらにそこから1進むとxに行ける頂点を(x0,x1,...,)とします。
すると、Aからxへの最短の道順の個数は、Aからx0までの個数、Aからx1までの個数…って感じ。
ABC020 C-壁抜け
- [二分探索,幅優先探索が難しい]
あるxが達成可能かを判定しよう！
xが可能ならx-1は可能なのは分かると思う。単調性があるってやつだね〜
最初は、黒を通る回数をできるだけ少なくして、出来るだけ最短手数で行けばいいって思ったんだけど、必ずしもそうじゃないたぷ…
S####
.###G
.....
みたいな時、最短で行くよりなんとなく.だけ通ってS->Gの方が良さそうなパターンもあるたぷ…
だから、x の値を二分探索で求めた
2020/06/21
ABC016 C- 友達の友達
- [set,重複は許さない]
ABC171 A~E
A- αlphabet
- [英小文字と英大文字,知らない関数]
解説放送3秒だけ見ました。 どうやら、is_lower,is_upperという関数がc++にはあるらしいです。すごいですね。
B- Mix Juice
- [ソート,最小化]
やすいのをK個買えば良い
C- One Quadrillion and One Dalmatians
- [26進数変換、バグ梅小宮]
10進数を2進数に変換するノリでやってあげればノリノリ。
D- Replacing
- [連想配列,和]
Bi を Ci に変えるたびに、a0が3個、a1が514個、a2が3個。みたいにやるのはめんどくさいです。
（計算量的にもね)
最初に全部の和を求めておきます(sum)。
biがciに変わる時、sumからはbi(biの個数)が引かれ、ci(biの個数)がたされます。この操作をするだけです。それぞれの数字が何個あるかは連想配列で管理してあげましょう。
E- Red Scarf
- [XOR,XORの性質]
XORの基本的な性質として、 K XOR K = 0 がありますね。
また、 K XOR 0 = K です。
（多分)
ABC147 D- Xor Sum4
この回で、XORワケワカランくて調べてたときに上の性質は知りました。結局其の性質を知っても上の問題は解けなかったんだけどね。
で、つまり、a[0] ~ a[n-1]までのXORを取ったものに対してa[i] のXORを取れば、a[0] ~ a[n-1] (a[i]は除く)のXORを取ったものが求められるじゃん。え、なめてるの？って感じで通しました。(E,でしょ？え、これで通るよね？でもEだよ？通らなかったらどうしよう…って思いながら提出するとACでした)
2020/06/22
ABC123 D-Cake 123
- [大きい方から何番目,優先度付きキュー]
結構頑張った。難しい。
まず、x,y,zがそれぞれ103を最大取るので、x * y * z通りの美味しさを全て列挙するのは無理無理無理無理カタツムリ(109列挙したら時間が無理で死ぬ)
なんとなく半分全列挙みたいな言葉が浮かんで、それは関係ないんだけど、とりあえず,Aから1個、Bから1個ずつとるx * y通りの組み合わせなら106個の組み合わせ（が最大）なので全部並べてソートも出来るな。ってことが分かった
当然ながら、美味しさが一番大きいものは、 Aから最大、Bから最大、Cから最大。
AとBから1個ずつ取ったx * y 通りの美味しさの組み合わせの配列（？？）(AB配列って言っとく)を昇順にソートしてやると、各Ciを使ったときに美味しさが一番大きい条件って,Ci+ABの一番大きいやつ。
これを z 個優先度付きキューにブチこんでやって、ってやれば解けた。（すごい)
C0,C1,C2,...,Cz-1に対して一番大きいのはAB[n-1]にCi( 0 <= i <= z-1)を足したものだな〜なイメージから行ける（俺は天才だからソレで行ける)
2020/06/23
ABC122 D- We Like AGC
- [DP]
ダメになるパターンを列挙して頑張る。 DPの配列に、1文字前,2文字前、3文字前のアルファベットが何かの状態をもたせる。
ARC089 D- Xor Sum 2
- [Xorの性質,尺とり法]
xorは、繰り上がりの無い足し算。
010と100のように、各bit桁ごとに、立っているもののかずが1個以下のとき
010 xor 100 = 010 + 100 と一緒。
2020/06/26
ABC145 E- All-you-can-eat
- [ﾁｮｯﾄﾖｸﾜｶﾗﾅｲ,最適化,分かったかも]
注文する料理の中で、時間が最も係るものを最後に注文すればいい。だから時間で昇順にソートしておくと良い。
ただのDPだけでは解けず
rep(i,n){ rep(j,t){ chmax(dp[i+1][j], dp[i][j]); int nj = j + p[i].first; if(nj < t) chmax(dp[i+1][nj], dp[i][j] + p[i].second); } int now = dp[i][t-1]+p[i].second; // ここが要 chmax(ans,now); }
int now = dp[i][t-1]+p[i].second;
が重要アル
こいつが、一個だけ食べるのに係る時間を無視して食える。みたいなことを意味している。
ABC133 E- Virus Tree 2
- [木,mod数え上げ]
解けた！！
どの頂点から色を決めて行っても一緒だろ（数え上げの経験から）
だから、テキトウに根を決めて、其の色を塗る。
BFSで次の頂点を見る。（この時の注目する頂点をvとする)
vの周りで、既に色が塗られている頂点を数えて、vをk-(今数えた数)通りで塗る。
って言うことをやっていきました。既に塗ったかどうかはboolの配列で管理しました。
ABC132 E- Hopscotch Addict
- [有向グラフ,グラフの拡張,ちょうどゴール]
始めて見るタイプの難しいグラフの問題でした。写経ACです。
頂点sから頂点tに、どうにかして３の倍数回の移動でゴールしたい
そんなときは、頂点に状態を持たせて、1つの頂点を3倍に拡張してやるといいらしいです。
まぁ、ちょっと理解あれだけど、知識増えたってことでヨシ。
2020/09/02
ARC013 B-引っ越しできるかな？
- [最適化,最小化]
それぞれの荷物について、縦、横、高さがありますが、どれが縦とか横とか別にどうでもいいので、用意したい箱の縦、横、高さを、縦が一番短く、高さが一番長くするようにしようかな。っていう解法。（証明不明）
つまり、入力で与えられる N, M, L を N <= M <= L とする。 N <= M <= L でないならば、適当にN,M,Lを入れ替えてやる。 そうして、N0 ~ Ncのうち最大のものが箱の縦の長さ。
M0 ~ Mc のうち最大のものが箱の横の長さ。
って感じでやれば解ける。
解説でもなんでもないな。
うーん、お気持ちを言えば、いったん全ての荷物について、どの辺を縦にして、どの辺を横にして、どの辺を高さにするか、向きを決めてやる。って感じかな。
各荷物の一番短い辺の長さを縦として採用したい！！！
みたいなね。
CODE FESTIVAL 2014 決勝 D-パスカルの三角形
- [パスカルの三角形もどき,ﾋﾗﾒｷ~]
パスカルの三角形を実際に書いてみたら、(1-indexed)で左から2番目の数は1ずつ増えていってることが分かるから、任意の数がパスカルの三角形に登場することが分かる。
具体的には、ある数AはA+1段目の左から2番めに出てきます（あ、答え言っちゃった）
dwangoプログラミングコンテスト B-ニコニコ文字列
- [部分文字列,数え上げ,ほんのひと粒の涙]
ｴｯﾄﾈ,この問題の答えの最大値は,5 * 104 の2乗なんだけど、それは232に収まらないのでlong long を使おうね。（そのときの入力は、2525252525...25(5万組の25)です)
この日の日記(11/10)
ABC066 D-11
- [ncm,包除原理(とまでは言わない?)]
まず,答えに影響するのは，a[i] == a[j] (i != j)となるようなa[i]という値ではなく，
iとjの値です．
どの数字が2つあるかっていうのは興味がなくて，同じ数字が，どれくらい離れた距離にでてくるのかということにしか興味がありません．
まぁ，どうにかして2つの被ってる値の距離を求めて，その2つの間にある数字の数を mid としましょう
(つまり, a[i], a[i+1], a[i+2], ... , a[i+mid], a[j] です(j-i-1がmid);
さて，ここまで書いた上で投げやりですが，解説PDFが分かりやすいのでこれを読んでください．
ちなみに，なんの数字が被っている．というのは実は簡単に知ることができます．
sum = a_0 + a_1 + ... + a_n;とすると，
sum - (n * (n+1) / 2) の計算結果の値が2つでてきています．
ABC005 D-おいしいたこ焼きの焼き方
- [たこ焼きのタコは食べれる,二次元累積和,実装神]
某んちょんさんのコードを写経しました．
コード
何が素晴らしいかって，面積vを0〜n * n でループを回すんじゃなくて，長方形の左上と右下（伝われ！）の4点を4重ループで回して，x1,x2,y1,y2を決めて,その時の面積を求めることで val[v]を更新する．っていうところがイケメンだなって思いました．
さて，二次元累積和って難しいですよね
ABC086 D-Checker
- [二次元累積和,反転GG,条件の変換,激難,市松お粗末]
困りました，このモンダイについての考察は大嘘を含んでいます．見るな
このモンダイ，まだ自力できてないけどニャン
何が感動するかって，(2 * k) * (2 * k)のサイズしか考えなくて良くなることもそうなんだけど，
白がx[i] , y[i]にあるっていう条件は，黒がx[i]+k, y[i]にある (もしくはx[i],y[i]+k)っていうのと同値であると変形できるんす！！
(すげー)
もう一個同値としては，x[i], y[i]に黒があるっていう条件は， x[i] - 2k, y[i]に黒があるっていう条件と一緒(y[i] - 2kでも良い)ってことなんすね〜〜.
つまりx[i], y[i] 黒 -> x[i]%2k, y[i]%2k 黒 って変換をしちゃおうってね！
こっから先の二次元累積和は，難しい．また今度．
ABC155 D-Pairs
- [二分探索，lower_bound, upper_bound, 二分探索の自力実装,むずかしめ，条件の言い換え]
解説動画からの引用的な雑書きになる．
K番目に来る数をxとすると, xはx未満の数がK個未満であるもののうち，最大の値と言い換えることができます．
たとえば，1,2,3,3,4,5,6 っていうのが遭って，K = 2だとしよう
x未満の数がK個未満であるもののうち，最大の値という条件を見ていこう！
K = 2 だよ
1は，1未満（0以下)の数が0個(< K)なのでOK
2は2未満(1以下)の数が1個(< K) なので OK
3は,3未満(2以下)の数が2個( == K) なので NG
よって，条件を満たすものの最大の値は2で,実際の答えも2です
次に,K=3のとき(もう一回数列貼っておくね)
1,2,3,3,4,5,6
1は1未満（0以下)の数が0個(< K)なのでOK
2は2未満(1以下)の数が1個(< K) なので OK
3は3未満(2以下)の数が2個(< K) なので OK
4は4未満(3以下)の数が4個(>= K) なので NG
よって，条件を満たすものの最大の値は3で，実際の答えも3だからOK~~
とまあ，この条件の言い換えが重要で，x未満の数がK個未満であるもののうち，最大の値という条件には単調性が生まれるんですよね（日本語知らん)， X < Y のとき，Yが条件を満たしていたら,Xも条件を満たしているんですよね
天才かよ．と思いました．
後は，x未満の数が何個あるか数えるパートですね．
これは，a_0 からa_1, ... ,a_nに対してそれぞれ何個あるかの和を求めます．
今,a_iについてa_i * a_j < x となるようなjの最大値を知りたいです!!
一回簡単のためにa_iは正の数としておきましょう．あ，あと数列aはソート済みってことにしといて．
はいじゃあ，a_i * hoge < x のとき，式変形をして
hoge < x / a_i ですね
つまり，x/a_i は条件を満たしてくれる，そして， x/a_i + 1 は条件(a_iとの積 < x)を満たしてくれません
x/a_i + 1 = searchとでも置いておきましょう．
はい．今，aがソート済みであるとき， search以上の値が最初に出てくる位置，はlower_boundを用いて求めることができますね．
これで，a_iに対して a_i * hoge < x となるhogeが何個あるかは求めることができます．
lower_boundで求まった位置をjとすると，a[j-1]までならa_i * a[j-1] < x なので，hogeはj個あります．
iを0からn_1までやって，hogeが合計何個あるかをtmp個としましょう
この時tmp < K だったら，xはx未満の数がK個未満であるものです．
ハイ次，さっきは，aが全て正の数だと言っていましたが，aに負の値が含まれているときを考えよう．
-5,-3, -3, -2, -1, -1, 0, 4 , 5 みたいなときや
まぁなんかテキトウに，x = 11とでもして a_0=-5)に対して，a_0 との積が11未満になるものの数を数えよう．
これをさっきと同じふうに search = (x/a_i + 1)としてしまうと，search = (11/(-5) + 1) = -1?になります(負の値の除算分からん)で，正の値のときと同じように，search以上の値が最初に出てくる位置(j)を求めると, j = 3 と出てきますね(a_j = -1)
でもでもでもでも，さっき(aが正だけのとき)は， j = 3 として出てきたら，
a_i * a_0 もa_i * a_1 もa_i * a_2 も全部x未満だったじゃん？でも今回は違うんだよ
だってほら，a_i (=-5) * a_0 (= -5) = 25じゃん
x = 11 じゃん．
25 > 11 じゃん
つまり，a_i < 0 のときは，aを右からみて何個取れるか，って考えなきゃいけないんだ！！
俺はここで実装つまらせて泣いて泣いて泣いて泣いてたんだけど,でも実はこれってupper_boundを使えばよくて(DA?GOの口調)...
aが昇順になってることから，まぁ二分探索で位置求めるのが楽っていうのはそれはそうです．
探す値が -1 っていうのは間違ってますね．
ここでは，a_i * (探す値) >= xとなってほしいのに， a_i * (-1) = -5 * -1 = 5 で，x(=11)よりも小さいです．
だからどうやら，a_iが負の時は，探す値を x/a_i - 1としなきゃいけないみたいですね(へー)
今回は，11/(-5) - 1 = -3 としてsearchが取れて，-5 * -3 = 15 > 11 なのでなるほど確かにそのようになっていますね．
-5,-3, ( * )-3, -2, -1, -1, 0, 4 , 5の中から-3を探す時，米印をつけた方の-3の位置を見つけて欲しいです．
なんでかっていうと,a_iが-5のときに a_i * hoge < x になるものは，
-5,-3, -3, [-2, -1, -1, 0, 4 , 5] のように[]で囲った部分でしゅ
だから，upper_boundで，-3以上となるindexのなかで最大のものを…(あれ？嘘じゃん),-3以下となる値で一番右の位置を求めないといけないじゃん．
ABC093 D-Worst Case
- [二分探索,良い位置,二項の積の性質]
面白いモンダイですね．
とりあえずまぁ，二分探索を使うということが分かったという前提（はい)でやっていきます
今，高橋くんよりスコアの低い人物がX人はokかngかを判定したいです．
X人に対して，1試合メと2試合目で何位だったかを考えると，1試合目では1位からX位（とちゅうでA[i]があるならX+1位まで)のX人,
2試合目では1位からX位（途中でB[i]があるならB[i]位を除いてX+1位まで)のX人としてあげるのがいいことは何となく分かると思います．
X位の人を使わないで Y位(X < Y)にしたって,スコアが大きくなるだけで損なだけだしね．
で，1試合目と2試合目の組？みたいなのを考えた時，1試合目で1位だった人は2試合目でX位ぐらい(2試合目として採用する順位の中で一番順位的に悪いやつ)だったことにしてって感じでやると，
X人についての1試合目のスコア * 2試合目のスコア っていうものの最大値を最小にすることが出来るっピ
まぁ，こんな感じで最大値の最小値が高橋くんのスコアよりモヒかければ，X人は達成出来る．って感じでやっていけばええんや．
がんばれ，俺は頑張った．
ABC182 E- Akari
- [まだ解説読んでない,分解，Lamp,実装がんばえ]
ランプを見つける度に上下を照らして，左右を照らして…ってやると脳がバグります（僕はバグりました)
そこで，ランプを2種類あると考えます．
左右のみを照らすランプと，上下のみを照らすランプの2つです．
H * W のマス目を2つ用意します．
1つは，左右のみを照らすランプを考えるようのマス目
もう1つは，上下のみを照らすランプを考えるようのマス目
それぞれのマス目の上で，左右のみマス目では，
ランプの隣が壁じゃなければ，そのマスの右もランプに感染させる．みたいなことをします．
すると，..o..#..みたいなマス目が(.は何もないます，oはランプ，#は壁)
..ooo#..に変化します．
次に，ランプの隣が壁じゃなければ，そのますの左もランプに感染させる．ってことをします．
するとooooo#..ってなります．
上下のみてらすランプがあるマス目でも，同じようなことをします．
この操作をした後に，H * W ます全部に対して， 左右のみランプ， 上下のみランプのマスのどっちかでランプとして感染済み(もしくは元からランプだった)なら，照らされるマスとしてカウントする．っていうことをやってやります
2021年1月11日
ABC188 F-+1-1x2
[DFS,深さ優先探索,数字操作,メモ化再帰] これ難しくないですか.難しいですね.
2021年 1月 12日
パナソニックプログラミングコンテスト (ABC186) E-Throne
[拡張ユーグリッド,extgcd,逆元]
S + X * K = α * N (α は1以上の整数)よなるような最小のXを求めよという問題.
X * K ≡ -S (mod N) を解く.みたいなノリっぽいですね.
ここで X ≡ -S * (Kの逆元) として解きたいなあ.みたいな感じなんだけど,ここから先が分からなくて解けなかった.
そのうち理解したくなったら蟻本の260pを見よう♡
ちなみに,逆元に関する知識として,
mod が素数じゃない時は,逆元が存在しないときもあるらしいよ.
素数じゃないときは,互いに素なら存在する.らしい!!!
2021年 1月 17日,解いた問題
ARC007 C-節約生活
- [bitDP,集合を管理するDP]
問題の概要
'oxoxooo'みたいなのを繰り返し使い,oとxが重なった部分はoにすることで,'ooooooo'にしたい.(ちょっとめんどくさい言い換え)
2021年1月19日解いた問題
ABC007 D-禁止された数字
[桁DP,MOD使わないぴょん,遷移4通り?,もらうDP]
K以下の整数の中で,4か9を含んでしまう整数は何通りありますか?
桁DPを頑張る.良かったら記事見て
2021年8月8日解いた問題
AGC053 A- ><again
[良い非負整数列,整数列の分解]
2021年8月10日解いた問題
COLOCON -Colopl programming contest 2018- C- すぬけそだてーーごはんーー
[嬉しい,素数の個数,全探索,bitDP,UnionFindではない]
2021年8月11日解いた問題
ABC195 F- Coprime Present
[嬉しい,素数の個数,bitDP,UnionFindではない]
昨日やったすぬけそだてーーごはんーーの制約が厳しい版です(情報提供・あさか，こいつは本番で通した．犯罪だね)．
ABC073 D- Joisino's travel
[ワーシャるフロイド法,next_permutation,bitDPによる巡回セールスマンっぽい]
ABC180 E- E - Traveling Salesman among Aerial Cities
[ワーシャルフロイド法,bitDP,巡回セールスマン]
Joisino's travelのように，next_permutationを用いていたら実行時間が間に合わないっすね．17の階乗は，10を8回以上かけているのでどう考えても間に合わないです．
2022年2月10日
久しぶりに競プロ解いた問題の解説書いたわあ(解説…?）
ABC226 D - Teleportation
[全探索、辞書型配列,比の約分]
- 各頂点から(自身以外の)各頂点へ、1つの魔法のみを使って移動する
- 1つの魔法であれば、何回使ってもいい
- 任意の頂点から、任意の頂点へ、上記のルールで移動するとき、魔法が最小で何種類あればいいかを求める問題
ABC232 C - Graph Isomorphism
[順列全探索,,nextpermutation,頭壊れる]
next permutationっぽいなコレ。こういう問題頭壊れるｯｽﾈ
2022年2月11日
ABC225 C - Calendar Validator
- [書けばわかる、サンプルがすべてじゃない、オーバーフローしない、灰diff]
灰色diffだけど、そこそこ難しい。サンプルが通っても勝ちじゃない
書けばわかるんだけど、行列Aを書くと、こうなるよ
4月3日
[01-BFS, 普通のBFSじゃTLE,斜め移動]
自分はこのTLEが出るところまでできましたが、TLEを取ることができなかった…力不足デス…（CV.チノちゃん) 普通の幅優先探索しようとすると、queueに入れて…って感じでまわしますよね。でもそれだとTLE…どうしてTLEになってしまうかは分かりません(ｴｰｯ！！(cv.はちわれ))
ABC246-F typewriter
[動的計画法、桁DP的な？文字列数え上げ、ncm,]
厄介な問題デス…
'a'と'b'のみの長さLの文字列と、'b'と'c'飲みの長さLの文字列の個数は一緒です。それぞれは干渉しません。
2020-04-04
ABC174 F- Range Set Query
Moの中身は分からないけど、とりあえずこれ参照しよう！ こーど 注意点として、C++を使っていたら cin や cout endlをしちゃうとTLEになります（うげ〜）
2022年4月11日くらい
ARC138 A-Lerger Score
[添字を持った配列、優先度付きキュー、だんだん選べるものが増えていくタイプ,ソート]
スコアをS+1にすると誤読していた。 1点以上上げれば良いのだから、Aにある要素を一つだけそれより大きいものに変えてやれば良い。
ARC138 B- 01 Generation
[0と1からなる数列の構築、構築、操作を逆に考える] 操作を逆に考えると、ヤル操作は、後ろの０を取るか、前の０を取ってFlipかの２通り。
後ろの０を取るのを優先してやって、空の文字列にできれば勝ち
ARC138 D-Differ by K bits
[XORの基底？] なんか頑張った気がするけど解けなかった。難しかった。よう復習。
ABC247 C- 1 2 1 3 1 2 1
[再帰、butilin_ctz, popcount]
naoyaさんのGCCのビルトイン関数メモが参考になりそう。
適当な再帰関数を書いてあげると通る。
ABC247 D- Cylinder
[DはdequeueのD,何が何個あるかが大事]
5を５個追加ってとき、5,5,5,5,5って追加するなじゃなくて、(5,5)を追加する。
ABC247 E- Max Min
[セグ木？うるせえよ。DP、状態を持つDP]
ABC247 F- Cards
[Lucas数、連続した2個のうち1個は取るやつ、リュカ数]
類題があった気がするけど忘れた。ブログを書こうね。
見たことがある感じ、カードの表裏は辺を貼るみたいなの典型なのかな？
UnionFindでくっつけて、みたいな感じなところは直感で出来たんだけど、島のサイズに対する答えの求め方がわからなかった。でもそれがLucas数ってやつになるらしい
注意点としては例えば5つに対して取る取らないを決める。ただし、連続して2回取らないをしちゃだめってトキ
xoxoxはNGです。みたいな感じな注意がある。でもそれもリュカ数で数えられちゃうらしい。すごい。
2022年4月13日
ABC236 F- Spices
[XORの基底、内部は分からない、類題あり、解説動画優秀、掃き出し法]
先日行われたARC138 D-Differ by K bitsの類題ってことで良いですか？良いですよ。
掃き出し法のわけが分からない実装ですが、
を見るとちょっとだけ「あー、そんな感じノコとしてるのね。知らんけど」ってなります。
for(int e : order){ for(int b : basis){ chmin(e, e ^ b); } if(e){ basis.push_back(e); } }
このコード、Twitterでのし袋さんがのけてたやつみたいな感じです。
これをすると、basisに配列 orderの中から基底が取り出せるらしい
2022年5月8日 日記
本気解説，書いた。親愛なる先輩へ，愛をこめて。
ABC248 F- Keep Connect
[連結DP, 連結状態,がんばれ,記事書いた]
連結DPとかいうのに初挑戦した。 気持ち，桁DPに似ている。絶対不可能な状態には遷移しないように注意しつつ，okな状態(連結な状態),非連結な状態みたいな感じ。 ただ，桁DPと違って，一度連結になったとしてもその後連結じゃないみたいな感じになるっていうのがややこしいところ。
AGC057 A- Antichain of Integer Strings
[凶悪二分探索,愚直死ぬ,わけわからん]
よく分からないけど，わかるのはWriterのmaspyさんが天才ってことだけ。
ゲームの思い出
ゲームの思い出の整理
今、25歳。最近はあんまりゲームをしなくなったが、思えば小学校に入る前、5,6歳の頃からPCゲームをしていたなあ、と。20年前も前なんだなあ。
ふとTalesWeaverのBGMを聴きながら、散歩してたら懐かしい記憶を文字起こししたくなった。
幼稚園時代
一番最初に始めたPCゲームはTalesWeaverだった（スペルあってるか不明)。四人兄弟の末っ子で、一番上が7歳上。つまりは、長男が12,13歳ぐらいの頃にTalesWeaverをやっているのをみて、自分も始めたのだと思う。PCゲーム英才教育だなあ。と感じる。
（そういえばあの頃は家に一台しかPCがなかった気がするが、長男はキャラだけ作ってすぐやめたのかな？それとも俺がPC独占してたのかな？）
最初に作ったキャラは鞭を使うキャラ(ミラ)、確か30レベルに到達したぐらいでやめた気がする。 その時の記憶はあんまりなくて、長男が忍者のキャラ（ナヤトレイ)を使っていた記憶がある。
どれくらいの期間遊んでいたかはわからないが、小学生になった時も少しはやっていた気がする。
小学生時代
1,2年生(たぶん)
1,2年生の頃にやっていたのは、チョコットランドかメイプルストーリーのどっちか。
チョコットランドは親友と一緒にプレイしていたが、親友は（親が）課金体質で、どんどん強くなっていくのが悔しかった。
メイプルストーリーを始めたのは、もしかしたらもう少し遅くで、小5とかかもしれない。 次男が友達とやっていた気がする。まだ冒険者しかなくて、初期の島から出るためにメイプルキノコを倒していた気がする。あんまり覚えてないなあ。確か最初の転職は、ローグになった気がするな。手裏剣を投げるのかっこいいよね。
カニクエとモンカニ(MC)でレベルを上げて、多分最初は一次MCをしてるとき,30レベルちょっと行ったぐらいで辞めた気がする。(モンカニは、30~50レベルの間でプレイできる一次MCと、51~70の二次MCで分かれていた気がする)
確か、頑張って雷手裏剣を入手したよね。それで、椅子取りゲームしよう！みたいな感じで知らない人に声をかけられて、雷手裏剣を落としたら盗まれて、それで萎えて引退したのかな？それとも、この頃は火・毒の魔法使いやってたっけ？
3~6年生(たぶん)
いろんなゲームをやったと思う。
アラド戦記・ロストオンライン・Tales Weaver・メイプルストーリー ・RedStone・チョコットランド
思い出せるだけだとこれくらいしかない気がする。もちろん他にも謎なフラッシュゲームもしてたけど。
小学校時代は、小学校の友達と放課後は毎日公園で遊んで、帰ってきたら毎日ゲームしてたな〜。（すごいエネルギー)
幼稚園時代からかいつからなのかは覚えていないけど、姉もPCを使うから、1日PCは1時間(30分枠を2回)っていうルールが決められてたなあ（ほとんど守ってなかったけど)
家庭共用のPCで、最初は超小さいデスクトップPC,次は家電量販店でのノートPC(インテルCeleron)を高１の4,5月ぐらいまでずっと使っていたのが懐かしい。 どれだけ動作がカクカクでもゲームを楽しんでいたよ。
メイプルストーリーでは、ゆうちょ銀行に入れていたお年玉を、課金のために1000円ずつ引き下ろして、その度に手数料100円とられていたね。たぶん手数料で1000~2000円取られてる。
ジパングで買えるバスタオルを強化して使うような時代だった気がする。
この時は、確かアランをプレイしていたね。50レベルまで行った気がするよ。 日本列島っていう武器を課金して買ったね。 その課金した武器をID・PWを知らない人に聞かれて教えて、盗まれたね。 萎えて辞めたね。
RedStoneは中学生時代かも。長男の友達がやってるって聞いて、やり始めた。結構大きな課金額3000~5000？のアイテムを買うとレベル効率とか移動効率がめちゃくちゃ早くなった気がする。自分では買ってないけど、回復役みたいな職業やればあげるよ！みたいな感じでゲームの人にもらったのかも。それか、ゲームやり始めた人には30日限定で配るとかあったのかも。
ロストオンラインは、ポータルで二次探索みたいなことをして、短い回数で目的の部屋に入るとたくさん報酬がもらえる。みたいな何かがあった気がする。 宝石（パール）とかがえぐい値段で取引されているゲームだったり、ジャンプしながら銃を撃ったり、アサルトとショットガンを持ち帰ることで高速射撃ができるようなそんなゲームだった気がする。
TalesWeaverは今回は、マキシミン(剣使うやつ)を使ってたね。 ギルドのナヤトレイの人、レベルカンストしてるマキシミンの人（織田信長代理)と出会ってよくチャットしてたね。懐かしい。 結構頑張ったよね、70レベルぐらいまでやった気がする。 虚無僧笠みたいな名前の帽子を忍者の里でゲットして、ステータスガチャ引きまくってたね。 荒々しい虎の魂みたいなアイテムも、地味にステータス結構上がって嬉しかったね。
何かに飽きるたび、オンラインゲーム、ランキングとかで調べて見つけたゲームを適当に遊んでた気がする。
中学生時代 ~ 高校時代
中学生前半
中１の頃は、同じクラスの子が4・5人ぐらいメイプルストーリーをプレイしていた。
テストの時期になると、銅の覚え方はカッパードレイク（メイプルのモンスターの名前）で、Cupper銅レイクみたいなこと言ってる学級委員長がいたな。懐かしい。
この頃のメイプルは150レベルぐらいまで余裕で到達できる時代だった気がする。（たぶんもうモンカ二はなくなっている)
そのあとは、アラド戦記を結構やった気がするなあ。
初めて大きな課金(5000円)をして、アバターを買ったような気がする。
中学生後半 ~ 高校時代
メイプルをしてた友人の家に行ったら、AVAをしていたね。たぶん中学2年か3年。
FPSとの出会いだったね。一番最初はよくわからず適当な部屋に入ったら、なんかめちゃくちゃゲームを教えてくれる優しい人がいて、フレンドにはなってないけど色々教えてくれたな〜。
初めてクランに入って、結構歳近い人がいたなあ。このクランのマスター（社会人）と高校1年の5月にはじめて会って、秋葉原でモニター買うの付き合ってもらったな。 秋葉原から最寄りの駅までモニター持って行って、最寄り駅（と言っても徒歩50分）から自宅まで自転車で帰ろうとしたんだっけ（諦めて親に迎えに来てもらった)
高校の夏頃か覚えてないけど、別の学生クランに入って、Twitterか何かで「前のクランの人」みたいな単語を使ったら秋葉原一緒に行ったクラマスがキレてLineのグループ追い出された気がする。変な思い出。
高校1年
時系列ちょっと戻るけど、4月か5月に、中学生時代頑張って貯めたお金を使って、初めて自分のデスクトップPCを買ったね。その後（届くの待ってる間?)クラマスと秋葉原にモニターを買いに行ったね。 PCが届いた時、父親に「こんなでかいって知ってたの？」って聞かれて、知らなかったけど「うん」って答えたよね。
PCが届いて１週間も経たずに、あなたは牛乳を溢しました。ドスパラが優しくてよかったね。直してもらえました。
夏、あなたは学生クランを探しました。破滅の始まりです。LeaPと出会いました。おめでとう。
https://ava0zeturin0.wixsite.com/ava-clan-leap
クランに入りたての頃は夏でした。 中学の友達は別のクランに入りました。そこには、ゆうやみ、それからナンバー2がいましたね。
LeaPに引き抜きました。
お盆には帰省があります。 あぜむんとランクマッチプレイ中、「ごめん、そろそろ宮崎行かなきゃいけない。抜けるわ」僕はランクマッチを放棄しました。
ごめんねあぜむん。
ふみやまとはせしんは、VCに来ず二人でずっと遊んでいましたね。
秋、BouchanがBANされたのはこの時期だった気がする。さよなら。 秋、東京ゲームショーに行きました。シェード、フェリア、Bouchan。何があったか全然覚えてないね。 TGSの後、しぇーどと秋葉原に行きました。俺はキーボードを見ました。欲しかったのはRazerのdeathadder?だっけ、橙軸のキーボードを探したけど、英字配列のキーボードしかなかったね。その夜調べたら、英字配列でも日本語が入力できるって知って、面白そうだから英字配列を買ったんだよね。英断だったよ。
たけ、百夜・・・何その名前、読めないよ。
そういえば、近所というほど近くはないけど、スーパーでバイトしてたね、4月ごろから10月ぐらいまで働いたね。 君は3つのヘッドセットを買ったよ。SteelSeriesのSiberia 350。Razerの側圧強い1万円ぐらいのヘッドセット、それからゼンハイザーのGameZero。 Razerのヘッドセットはクラスメイトにあげたね。ゼンハイザーはボロボロで捨てたよ。 SteelSeriesのはメルカリで売ったね。
(ふじあつ、俺がラーメン屋行くとき通話繋いでくれたね。元気かな)
高校2年
AVAはこの頃Dimacoが流行ってたんだっけ、ざくろと壁打ちしてた気がするな。 確か、Steamとかいうものの存在を知って、OSUだったり、H1Z1をしたね。
はせしんとはたくさんH1Z1をした気がするな。
夏
かいとと、東工大のオープンキャンパスに行ったね。 東工大のオープンキャンパスの前に、私は靴を買いました。ABCマートかな。
持ち歩くのが面倒だから、東工大のどっかの部屋で説明を聞いた後、持ち帰るのが面倒だから置いて帰りました。ありがとう東工大。
この頃はごちうさが流行ってたから、オープンキャンパスの後秋葉原でうさぎのポーチを二人で買ったね。（ごちうさのあのお父さんのうさぎの名前ど忘れした）
かいと、俺は1年浪人したけど、大学の学部も学科も学年も同じだったね。ありがとう。留年してくれて。 再開した時、俺のうさぎのポーチはえぐいボロボロだったね。
この頃からかな？かいとのクラスメイトのLineのグループに入ったね。あさかと一休とデブとゴロリとメガネの偉い人。
PUBG Mobileいっぱいしたね。俺が浪人した時もしたね。（あれ、この頃はPUBG Mobileでてないか?)
秋
塾に入学したね。PCケーブルを学校のロッカーにしまって、スマホをジップロックに入れて土に埋めようとしたね。
土に入れるのが面倒で玄関に放置してたら、いつの間にか消えたね（どっかの隙間に入った）。
それから、あなたは大学3年の夏まで携帯電話を2度と持ちませんでした。
卒業式の最中、ふみやまとはせしん、通話してくれたね。スーパーで煮干しの写真撮って盛り上がってたね。
高校3年 夏〜
あなたは塾を辞めましたね。きっかけはクラスメイトの友人が「辞め方がいいよ。その塾」と言ってくれたことでした。
ありがとう。
僕は久しぶりにPCを取り出して、オープンレックで色んな配信者を漁ってましたね。9月ぐらいかな、波にだいぶ乗り遅れたけど、PUBGをあぜむんに買ってもらいました。遊んだなあ。 受験が終わって（落ちた）、そこで知り合った人とドライブに行きましたね。ご飯奢ってくれてありがとう。お元気ですか。
浪人時代
ファミマでバイトしたね。（３ヶ月）夏は駿台の予備校にバイト代で行きました。有名な先生に会えて嬉しかったね。 Twitterの人にもあったし、何やってんだろうね。 PCは基本しまってたね、偉いよ。あさかたちとPUBG mobileいっぱいしたね。
大学時代
夏、帰省して秋葉原に行って、また大きい物（今度はデスクトップPCのケース）を買ったね。最寄り駅まで迎えに来てもらったんだっけ？
結局その後、家から静岡までPCケース発送したね。店で送ってもらえよ馬鹿。
大学1,2年は、一休、あさかといっぱいCSGOしたね。デブはめちゃくちゃ強くなってたね。(呼称が本名なのででぶって呼んでます) いっぱい課金したし、あさかは3万のナイフを盗まれたね。注意力散漫、被害額三万 SAY。
一休、このゲームは頭に当てるだけ。
風呂上がり急いでバスタオルだけ巻いて試合してたら顔から血がめちゃくちゃ出てきたね。びっくりしたね。初めて救急車に乗りました。
大学2年の後半は、しらすとこいちゃんといっぱいApeXしたなあ。あんまり強くならなかった。 野良で遊んでたら、台湾人のaiちゃんって女の子と仲良くなったね。半年前秋葉原で会ってきたよ。可愛かった。
大学3年のときは、研究室配属がありました。PSO2を始めたての頃です。男なのにめちゃくちゃ可愛い女声を出すメンバーと、声がめちゃくちゃ可愛い女性がいましたね。研究室配属で希望のところに行けなくて、やけ酒をキメて、慰めてもらいました。優しい人たちでした。 PSO2はあんまり記憶がないね。
研究室配属された後は、結構忙しくなりそうなのもあるし、自作したデスクトップPCがウンチすぎるのもあって、あんまりゲームしなかった気がするね。 スマホに放置少女入れて、4,5ヶ月ぐらいは遊んでた気がする。
大学4年はほぼゲームしていないんじゃないかな？どうだっけ。
社会人1ねんめ
入社して2ヶ月、デスクトップPCを買いました。 名前忘れたけど、MMORPGを中学の友達（AVAを教えてくれた人）とやったね。2,3ヶ月ぐらい。
Albion onlineだ。
あとはCSGOだったり適当なことを1年ぐらいしてたね。 TalesWeaverも久々にちょっとやったけど10時間もやらなかったね。思い出補正かな。
社会人2ねんめ
あんまり記憶がないなあ。9月末ぐらいに仕事嫌になって、カードショップシミュレーターをやったね。 その１週間後ぐらいにMMORPGがしたくなって、新作のMMORPGをやったね。Throne and Liberty。ギルドの人、いい人たちばっかだったけど、すぐ人減ったね。 １ヶ月半経った頃には半分ぐらいに人が減って、引っ越すからプレイできなくなるよ！って言った1ヶ月後にギルドはほぼ解散してギルド名変更。 年が明けて、２週間。女の子がクランを抜けると、誰もチャットしなくなったね。 明日インターネット開通するけど、もうみんなプレイしてないんだろうなあ・・・。
これから
VRChatでもしようかな。人と出会いたい。 まずはThrone And Libertyちょっと開いてみて、まだプレイしてる人いたらちょっとだけ会話してみようかな。
エンジニアキャリアでも振り返ってみるか
エンジニアキャリアでも振り返ってみるか
目的
どうせ自分が社会人一年目で何してたとか忘れてるから、備忘として
学生編
入学前 vimを知る
大学は情報学部のある学校へ。学科はCS系（情報学部の中でも文系・理系っぽい感じで分かれていた)。 斜め45度アイコンの人に浪人時代AtCoderを紹介されていたので、大学入学の１ヶ月前ぐらいにAtCoderを始めてみた。
Twitterで大学の人と絡んでいて、ツイキャスでAtCoderをしていた。 At Coderの提出エリアに直書きコーディングしていると、大学の先輩から「Vim使うといいよ」と言われたので、Vimを使うようになった。
大学入る前に準備しておくのはノートPCとPCのセットアップ(vimのインストール)らしい。
ゲームを作る授業
競プロerは１ファイルにコードを書くことしかしないので、classとか何みたいな感じで、複数に跨ったコードを書くことができません。僕もそうです。
大学1年か2年の頃に授業で、迷路ゲームを作る機会がありました。 その時はテンプレートであらかじめ迷路ゲームのシンプルなものが与えられ、オリジナル要素を加えるというものだったので、全部のファイルを確認することはしませんでした。そこそこコードは書いた気がするけど、全然コードを書いていない気もしている（ほぼ何も覚えていない)
インターン
大学3年時にインターンには２つ参加しました。 一つはリモートで1か2週間。なんかフレームワークを使ってゲーム作った。数百ファイルぐらいあったんだろうけど実際に触ったのは10にも満たない。（なんなら２、３ファイルかも)ぐらいで、ほぼ記憶に残っていないが、この時も複数のファイルに跨って仕事をする業務プログラミングの感覚は訳もわからないまま進んだ気がする。コミュニケーションも取りづらくてきつかった。
もう一つは対面で１週間ぐらい。インターン生が自分含めて三人ぐらいいた。pythonとLINEを使ってなんかした。この時は0からプログラミングだけど、結局1つのファイルで全部完結させてしまったので競プロの延長。
日常
趣味の開発とかはほぼしていなくて、友人が作ったDiscord bot の使い方を聞いてコードもらってたぐらい。
時々キラキラエンジニアに憧れて、言語勉強本を買ってみたりもしたけど、環境構築でつまづくことが多くてキラキラすることはできなかった。輝いているのはにぼしっていう名前だけ。（名前すら輝いていないよりマシ）
学生編 総括
- vimを知った
- 競プロをしてた
業務開発はしていない(体感)
- 業務開発に近いことをできる環境はちょっとあったのかもしれないけど、当時は業務開発がどんなものか知らなかったし、体感的には業務開発の経験は0だと思っている。
- ただ、情報学部系以外の競プロerよりかは謎のコードに触れる機会はあったと思う。（趣味開発をしている人は除く）
資格は何もとってない
社会人編
1年目 バックエンドエンジニア?
と言いつつAPI開発はしなかった（既にできていたから)。 だからAPIを新規に開発する方法（ルーティング？）とかもわからない。
Loggerを作ったり、ユニットテストのコード書いたりを研修でやった。
後はサーバで動かしているコードをdocker化したり（他プロジェクトはdocker化されてたからまねるだけ）。なんかあんまこれがバックエンドか！みたいな経験はしていない気がする。
Rustのロジック書いたり。
振られたタスクをこなす1年だった。
資格は LPIC Level１ 基本情報 情報セキュリティマネジメントをとった
2年目 フロントエンジニア?
何かフロントエンジニアっぽい感じになってた。（チーム移動。)
って言ってもまだほぼHTMLとかCSSは触っていなくて、PHPのロジックちょっといじったりORMのSQLクエリ（日本語正しいかわからん）を修正したり。
アプリがあるからそのコードもちょっと触ったりした。
試験は人間が直接やる感じなので、テストコードは書いていない。
MVCモデルとかいうのを少し学んでなんとなーーくのイメージはついた。これが業プロか！っていうのを少し感じたかも。
後はバックエンドの時もそうだけど、ログ調査とか、新しい環境を作るためにインフラとゴニョゴニョして...みたいなこともしている。
総括とお気持ち
割とコード改修以外の、他部署の人間と連携して、みたいなタスクは、毎年やっているタスクだったり、前任者を真似たりみたいなことが多くて、人がやった時のメモ必死で探してなんとなーくでこなしている。
コードの改修は泣きながらやっているし、javascriptとかHTMLとかCSSを触らなきゃいけなくなった時は頭から精子出して濃い涙を流している。
ずっと同じような仕事するってよりかはログ見たり試験作ったりたまにコード書いたり、色々やっているような印象を受けている。だからぶっちゃけどこ行っても何やれって言われてもやろうと思えばできるような気がしている。一方で、Rustのコードで設計から実装まで全部やってねーみたいなこと言われたら泣く。ロジックの外側の実装が泣くほどわからない。
学ぶことがなくなったり、昇給幅が猿のちんこになったら転職したいなって感じがする。 自分で理解できないコードを部下が書いている。みたいな状況は嫌なのでマネジメントにはまだ行きたくないし将来行きたいかどうかもわからない。 言語はどうであれ「何もないところから、設計ー実装ーテストまで全部やってねーみたいなこと言われてもできる」みたいな強い人になりたい。
あとがき
書きたいこと書こうとすると、事実だけじゃなくてお気持ちとか主観がめちゃくちゃ入ってきて、自分語り始まっちゃう。
【呪術不要】にぼしのライブラリ公開！！オムライス編
前提
この記事はワンピースのネタバレを含みます。最新話を追っていない方、単行本でワンピースを読んでいる方は、この記事にネタバレが含まれていることを承知の上お読みください。
この記事はバカが作るオムライスではありません。私はAtCoderの水色コーダーです。 今日は、私の料理ライブラリの中から、オムライスのレシピを紹介します。絶対に周りに人がいる状態で真似しないでください。やめられなくなってしまいます。
はじめに
シャンクスは右腕を失くします。
材料
ライス用
- 米 一合分よりちょい少なめ(お腹いっぱいになることが幸せとは限りません)
- 玉ねぎ 0.5玉 (仮に今月パチンカスになったとしてもパチンコの玉での代用はできません。っていうか、パチンコの玉を持ち帰ってはいけません)
- 塩胡椒 超々(体に悪くなさそうな程度)
- ソーセージ3本ぐらい (ポークピッツでの代用不可)
- バター 適当(多分多ければ多いほど美味い)
- ケチャップ そこそこ(赤ければいいというわけではありません)
オム用
- 牛乳(一口分ぐらい。←口に入れて計量してはいけません)
- バター 適当(多分多ければ多いほど美味い)
- 卵 2~3個
本編
- 玉ねぎをかっこいい包丁でみじん切りにします
- ソーセージと一緒に炒めます
- 塩胡椒を適当に
- 米とバターを入れます
- ケチャップを入れます
- ルフィのおじいちゃんであるモンキー・D・ガープは黒髭海賊団に捕えられます。
- そろそろ持ち手をつけましょう
- 塩胡椒も入れます
- ライスはこれで完成です。
- 卵を混ぜます。牛乳も少し入れるといいらしいですよ。
- オムを作って完成です。
終わりに
赤髪海賊団はキッドの船とバルトロメオの船を沈めます。
モザイクなしのオムライスが見たい方は下記のリンクから私のチャンネルをフォローしてください。 Eve&Zoro channel 🐱 - YouTube
浴槽で全裸になってバリカンで髪を切っていた俺、トラックに轢かれて異世界にしてしまう。髪型が変だから切ってやる？今更言われてももう遅い。バリカンがあるので結構です。
バリカンの魅力
早起きして、髪切りたいなって思ったときノータイムで散髪できる（美容院の予約や移動を考えなくてよい！）
バリカン代があれば髪を切れる！(2,000円程度のを使っている)
クソバリカン小説
新卒1年目を終えたので超大物子役になったつもりでchatGPTと20往復会話したかった。
1往復目
にぼし
２０２３年度が終わり、私はIT企業で社会人生活を１年終えました。 新卒１年目が終わったのです。 さて、ネットで面白い記事でも書いてやろうと思うわけです。 僕は今から超大物子役だった。という経歴を持っているようなノリで新卒１年目でした感を出します。 インタビュー形式で僕の新卒１年目を聞き出してください。 分量は質問と回答で雑に4000文字ぐらい書けばいいかんじですかね」
chatGPT
インタビュアー：はじめまして、ありがとうございます。新卒１年目で超大物子役だったということですが、具体的にはどのような経験をお持ちなんですか？
新卒：はじめまして、ありがとうございます。そうですね、実は私、子役としていくつかの映画やドラマに出演していました。その中でも特に注目された作品がありまして、それが私の新卒１年目にも影響を与えたと感じています。
インタビュアー：なるほど、それは興味深いですね。子役としての経験が、新卒１年目の仕事にどのような影響を与えたのでしょうか？
新卒：まず、子役としての経験から、プレッシャーに対する耐性を身につけることができました。撮影現場では常に周囲の期待が高く、一発で演技を成功させなければなりませんでした。そのため、新卒１年目の仕事でも同様に、プレッシャーの中で冷静に対応することができました。
また、子役時代には多くの人と協力して仕事をすることがありました。監督や共演者とのコミュニケーションやチームワークが不可欠でした。この経験から、新卒１年目の仕事でも積極的にチームに貢献し、他のメンバーと協力して成果を出すことができました。
インタビュアー：なるほど、それは非常に役立つ経験ですね。では、具体的にどのような仕事をしていたのでしょうか？
新卒：私はIT企業でエントリーレベルのポジションに就いていました。主にソフトウェア開発のプロジェクトに関わっていました。プログラミングやテスト、そしてクライアントとのコミュニケーションなど、幅広い業務を経験しました。
インタビュアー：なるほど、それは挑戦的な仕事ですね。子役としての経験と比べて、新卒１年目の仕事で特に苦労したことはありますか？
新卒：はい、もちろんありました。特に挑戦的だったのは、技術的な知識の不足でした。子役時代には演技に集中しており、ITの知識はほとんどありませんでしたので、最初の数ヶ月は学習の過程でした。しかし、その過程で先輩たちから多くの助言や指導を受け、徐々に成長していくことができました。
また、プロジェクトマネージメントやデッドラインの厳守など、ビジネスの側面も新たに学ぶ必要がありました。しかし、子役時代に培ったマネジメント能力や時間管理能力が役立ちました。
インタビュアー：それは素晴らしいですね。最後に、今後の
2往復目
にぼし
ちゃうねん。俺が新卒一年目だから、回答をするのはお前じゃなくて俺やねん。 ええか、まずはあんさんがインタビュアーとして質問をする。 そしたら俺が回答をする そしたらあんさんがまた質問をするねん。ええか？ ほな、最初からや
GPT
了解しました。では、インタビューを始めさせていただきます。
インタビュアー：はじめまして、ありがとうございます。新卒１年目で超大物子役だったということですが、具体的にはどのような経験をお持ちなんですか？
3往復目
にぼし
子役時代のことはインタビューしなくていいよ
GPT
了解しました。では、子役時代については触れず、新卒１年目の経験について話していただけますか？
4往復目
にぼし
質問がざっくりしすぎているね。 君はベテランインタビュアーになりきりたまえ
GPT
了解しました。では、もう少し具体的な質問をします。
インタビュアー：新卒１年目として、IT企業での仕事について教えていただけますか？具体的には、どのようなプロジェクトに関わりましたか？
5往復目
にぼし
あんまり仕事の中身か聞かれるの微妙かもしれない
GPT
理解しました。では、仕事の中身についてではなく、新卒１年目としての一般的な経験について聞いてみましょう。
インタビュアー：了解です。では、新卒１年目として、特に印象に残っている出来事や経験はありますか？例えば、何か挑戦的だったことや成果を挙げることができますか？
6往復目
にぼし
業務中の話で印象に残っている出来事だと、チャットツールで上司が怖いと感じる。とかかな。
横着しないでください。ってチャットが飛んできたときは死のうかと思いましたよ。ハハハ
GPT
わかりました。それでは、そのような印象に残る出来事についてお話いただけますか？
インタビュアー：新卒１年目として、業務中に印象に残る出来事があると仰っていましたね。チャットツールで上司から何か怒られたり、指摘されたりした経験があったそうですが、その具体的なエピソードについて教えていただけますか？
7往復目
にぼし
思い出したくもない。
GPT
わかりました、申し訳ありませんでした。では、他の話題に切り替えましょう。
インタビュアー：そうですね、そのような経験は避けた方が良さそうですね。では、新卒１年目として挑戦的だったことや成果について、もう少し明るい話題でお聞きしてもよろしいでしょうか？
8往復目
にぼし
先週あったフィードバック面談で、もともと入社時もそこそこ評価が高かったけど、最初から評価高いのにもかかわらずちゃんと1年間で成長してくれな。って言われたのが嬉しかった
GPT
それは良いフィードバックですね。成長を評価されることは、新卒１年目として非常に意義深いことです。そのフィードバックについて、もう少し詳しくお聞きしてもよろしいでしょうか？どのような点で成長が見られたのでしょうか？
9往復目
にぼし
User どんな点で評価されたんだろ。確かにあんまり聞いてなかったかも。 でも、業務内容を選り好みせずにやっている感はあったから、そこが社会人的には評価がよかったのかもしれないね。 後これは、今後の成長という面で言えば、質問するのに臆しないようになりたいな。
GPT
確かに、業務内容を選り好みせずに取り組む姿勢は社会人として評価される重要な要素の一つですね。それがあなたの成長につながったと考えられます。
また、今後の成長に向けては、質問することに臆することなく、積極的に学び、成長していくことが重要です。自分の不明な点や課題を素直に質問する姿勢は、周囲からの信頼を築く上でも大切な要素です。
フィードバック面談で評価された点や今後の成長に向けての意識を、しっかりと持ち続けることが、より一層の成長につながるでしょう。
10往復目
にぼし
あれ、もうインタビュー終わり？
GPT
申し訳ありません、会話が少し途切れてしまいましたね。まだ続けて話したいことがあれば、何でもおっしゃってください。
11往復目
にぼし
ｼｭﾝ
GPT
もし何か他に質問や話したいことがあれば、お気軽におっしゃってください。私はいつでもここにいます。
後記
いつでもどうぞ。私はここで待ってますから。
ツボ男かな
どこに行きますか？
事実
今日は、仕事が終わって、ホットモットに行った。 カツカレー、肉野菜炒め、唐揚げ弁当（おかずのみ）
15分ぐらい待ち、受け取り、チャリに乗る。
起きて、また寝て人でなし。
チャリに乗って漕ぐ、漕ぎだした。俺のチャリは動き出した。
少年とすれ違った、その瞬間俺の人生は色づき始めた。
第一章 出会い
少年（ぽっちゃり）「ドコヘ行きますか？」
俺（げっそり）「うわぁ！！！びっくりした！！」
チャリを止める。そいつはiPhoneを両手に持ち、祈りをささげるようなポーズをしていた。
チャリを止めた、でも、でもこいつやばいやつだ、逃げろ！！！！
俺はチャリを漕ぎ始めた。
少年（Pocchari）「ドコヘ行きますか！！！」
所感・感想
なんだったんだあれ。中国人っぽいかんじのかおつきだったな。
どこに行きますか？
あれはいったい、何だったんだろう。
どこに行きますか？（Shall We？）
私たち、今からデートに行くわけですけど、どこに行きますか？
先輩、今日お昼どこに行くんですか？
どこに行きますか？（Wakuwaku)
貴方はこれからどこに行くんですか？（興味）
どこに行きますか？（Help！）
私は行きたいところがあります、そのためにはどこに行きますか？（無茶）
人類の果て、未来
我々日本人、いや、地球人は、どこを目指し、どこへ行くのだろう。
IT,AI, chatGPT3.5、Pikumin4 、コロナ、大阪万博、積立NISA、少子高齢化社会。
少年は、私たちが目指すべき未来について、問いかけてきていたのかもしれない。
